KT Aivle School 에이블스쿨 기자단] 8.28(월) ~ 9.3(일) 서울교육공모전 마무리 & 데이터분석 & 교육선발

이번 주의 스케줄
- 데이터 분석 수업 --> ADsP 내용과 겹치는 부분이 있어서 이해에 도움이 되었다
- 서울교육공모전 마무리
- 현재까지의 셀프 테스트 점수
- 교육 선발, 아쉽게 회식은 불참ㅠ
- 코딩 복습
이번주 후기
데이터 분석 수업으로만 이루어진 주였다.
ADsP를 공부했어서 이해를 하는 데에 살짝 도움이 되긴 했지만 통계학과나 수학과 출신에 비하면 미약한 지식...
데이터 분석에서 코딩은 구현을 위한 도구이고 통계 지식이 더 중요할 수 도 있을 것 같다는 생각이 들었다.
핵심 개념 : 카이제곱검정, t검정, anova 분석, 피어슨 상관분석에서 p-value 해석!
p-value 0.05 미만일 때 채택하는 대립가설은 어떤 것인가
p-value 0.05가 기준선임은 확실히 기억해두면, 다른 부분은 헷갈릴 때 귀무가설이 무엇이지만 확인하면 손쉽게 문제를 해결할 수 있을 거라 생각한다

드디어 수업과 병행하던 공모전을 마무리 했다!!
그동안 "수업 중간 쉬는 시간 & 점심 시간"에도 공모전 준비에 시간을 투자해서 정말 힘들었는데 이제 다시 쉬는 시간에는 쉴 수 있을 거 같다 휴..


현재까지의 셀프 테스트 점수
100점 흐름은 계속 유지하자!!

교육선발~~
AIVLE School에서 머신러닝 교육에 들어가기 미리 들어두면 좋을 거 같아 신청해둔 교육에 선발되었다
좋긴하지만... 이 일정으로 반 회식에 참여 못하는 거는 아쉬운 포인트
지금 코딩이 거의 노베이스 상태라 앞으로 참여할 수 있는 교육이 있다면 적극적으로 참여하려고 한

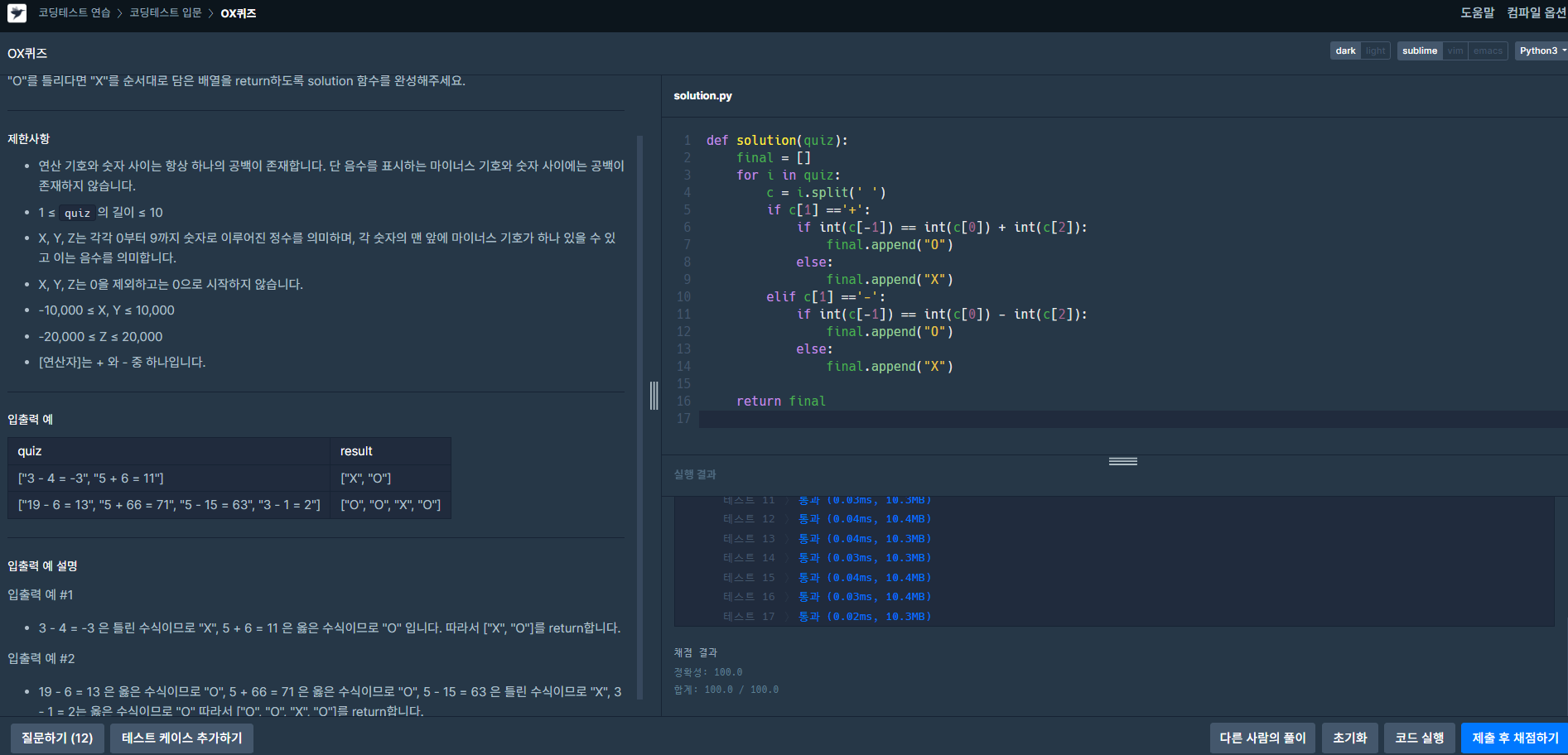
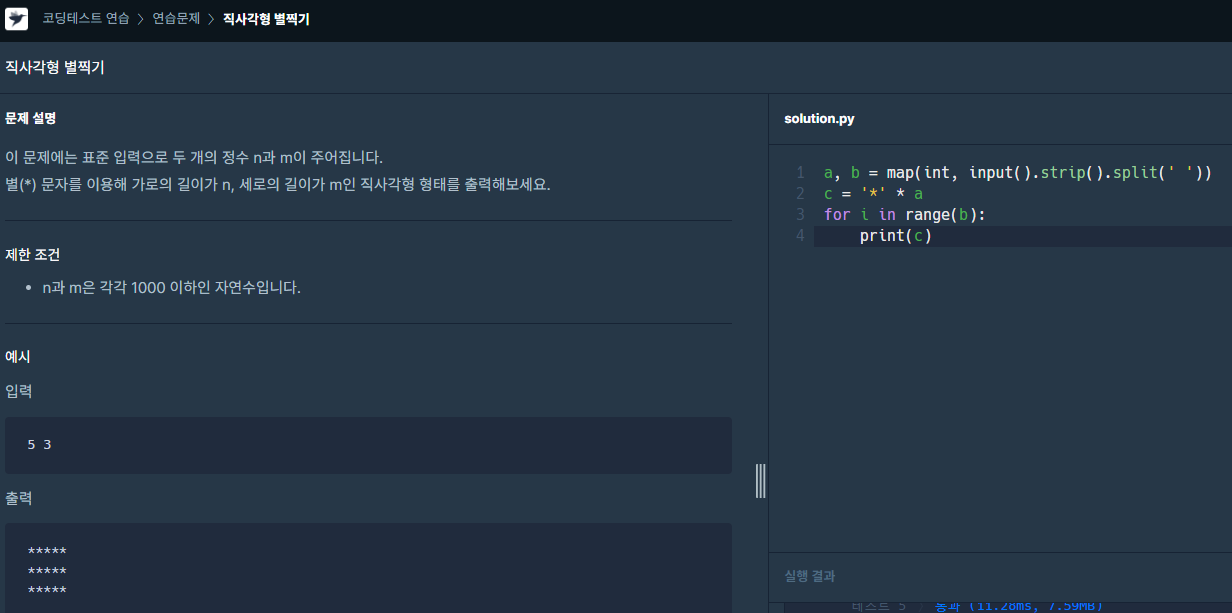
이번주 프로그래머스 문제풀이
매주 일요일 내가 리더로 진행하는 스터디를 통해 꾸쭌히 프로그래머스 문제를 풀어가는 것이 큰 도움이 된다고 느끼고 있다.
참여원이면 가끔 불참했을 수도 있는데 리더라 한 주도 빠지지 못하니 강제성이 부여되어 더 열심히 할 수 있다고 느낀다.
돌아가며 자신들의 코드를 발표하는데, 다른 사람 코드를 보고 설명을 들으니 시야가 넓어지는 느낌도 받고 있다.
이번주 코딩 복습!!
| 컬럼 정보 | 데이터프레임.columns |
| 컬럼 이름만 리스트에 담아 조회 | list( 데이터프레임.columns ) |
| 데이터프레임 조건 조회(loc) | 데이터프레임.loc [ (데이터프레임['컬럼명']==1) & (데이터프레임['컬럼명'] <=10) ] |
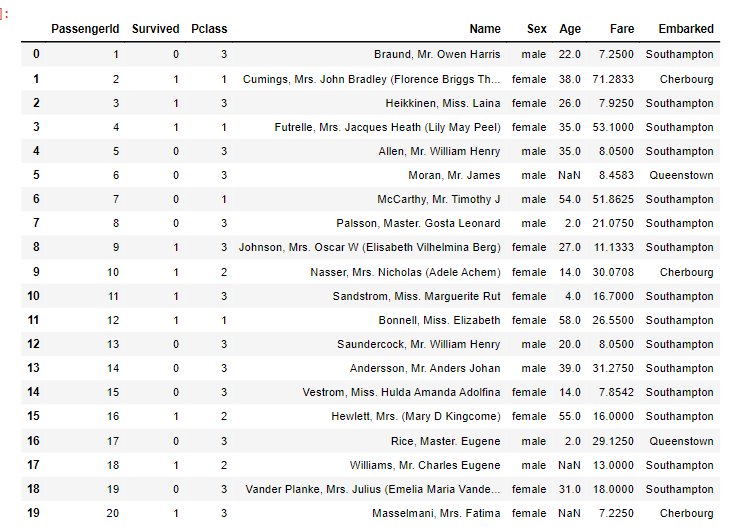
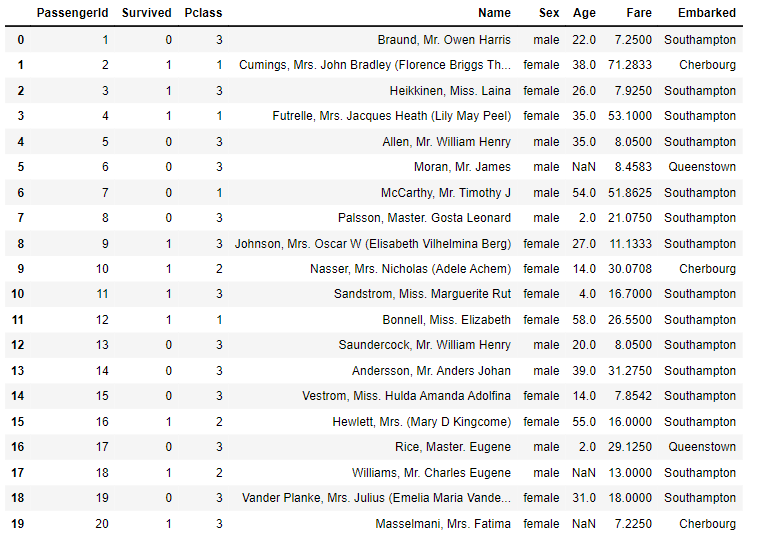
| 데이터프레임 조건 조회 | male_age = 데이터프레임.loc[ 데이터프레임['컬럼명'] == '원하는 데이터', '컬럼명'] female_age = 데이터프레임.loc[데이터프레임['컬럼명'] =='원하는 데이터','컬럼명'] 실제 코드 male_age = titanic.loc[titanic['Sex'] == 'male', 'Age'] female_age = titanic.loc[titanic['Sex'] =='female','Age'] titanic['Sex'].value_counts() |
| 결측치가 아닌 값 조회 | 데이터프레임.loc[ 데이터프레임['컬럼명'].notna() ] |
| 특정 수치 사이값 조회 (ex) 10 ~ 20 사이 값 |
데이터프레임.loc[ 데이터프레임['컬럼명'].between(10, 20) ] |
| 데이터프레임.loc[ (데이터프레임['컬럼명']>=10) & (데이터프레임['컬럼명'] <=20) ] | |
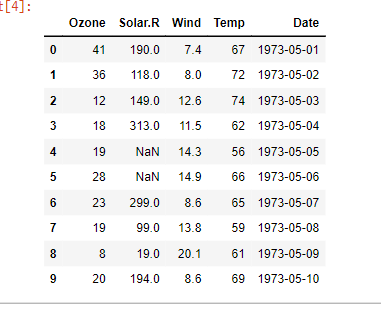
| 날짜 데이터 조회 | 데이터 프레임.loc['컬럼명'].isin( [ '날짜', '날짜' ] ) 실제 코드 air.loc[air['Date'].isin(['1973-05-01', '1973-06-01', '1973-07-01', '1973-08-01']) ] |
| 데이터프레임 값 변경 | 데이터프레임['컬럼명'] = 데이터프레임['컬럼명'].map({"원본 데이터" : "바꿀 데이터", "원본 데이터" : "바꿀 데이터"} ) |
| 데이터 값 변경 pd.cut | 데이터프레임['컬럼명'] = pd.cut(데이터프레임['컬럼명'], bins=[-np.inf, 30, 100, np.inf], labels = ['L','M','H']) |
| 데이터 값 변경 np.where | 데이터프레임['컬럼명'] = np.where(데이터프레임['컬럼명'] =='데이터값', 0, 1) |
| 데이터프레임['컬럼명'] = 데이터프레임['컬럼명'].replace({'데이터값': 0, '데이터값 : 1}) | |
| 데이터 합치기 Join, merge |
pd.merge( 데이터프레임, 데이터프레임, on ='컬럼명', how = 'left') |
| 정렬 sort_values | 데이터프레임.sort_values('컬럼명', ascending = False) |
날짜 데이터
| 날짜 형식으로 변경 | 데이터프레임['컬럼명'] = pd.to_datetime(데이터프레임['컬럼명']) |
| 연 데이터 추가 | 데이터프레임['Year'] = 데이터프레임['컬럼명'].dt.year |
| 월 데이터 추가 | 데이터프레임['Month'] = 데이터프레임['컬럼명'].dt.month |
단변량 분석_숫자형
| 평균 | np.mean(데이터프레임['컬럼명']) |
| 중앙값(중위수) | 데이터프레임['컬럼명'].mean() |
| np.median(데이터프레임['컬럼명']) | |
| 최빈값 | 데이터프레임['컬럼명'].mode() |
| 기초 통계량 전체 출력 | 데이터프레임.describe(include='all') |
| 숫자형 시각화 | |
| 히스토그램 | 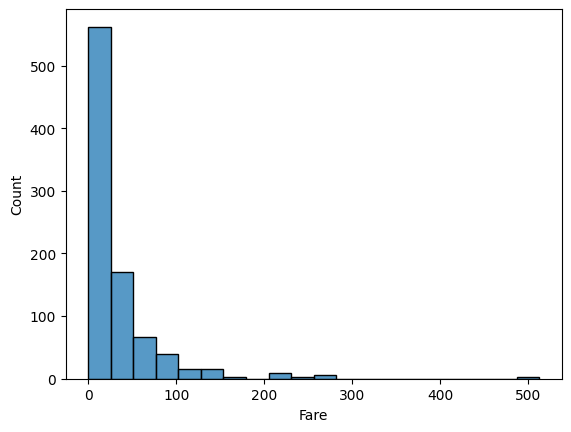 |
| plt.hist(데이터프레임.컬럼명, bins= 갯수, edgecolor = '색상') plt.xlabel('컬럼명') plt.ylabel('컬럼명') # bins 값을 통해 구간 갯수 조정 |
|
| 밀도함수 |  |
| sns.kdeplot(데이터프레임['컬럼명']) | |
| 히스토그램 & 밀도함수 함께 표기 |  |
| sns.histplot(데이터프레임['Age'], kde = True) | |
| 박스 플랏 |  |
| plt.boxplot(데이터프레임['컬럼명']) | |
단변량분석_범주형변수
| 범주별 빈도수 | value_counts() : 범주의 개수와 상관 없이 범주별 개수를 계산 데이터프레임['컬럼명'].value_counts() |
| 범주별 비율 계산(응용) | 데이터프레임['컬럼명'].value_counts() / 데이터프레임.shape[0] 데이터프레임.shape 함수의 첫 번째 값이 row 값임을 활용 |
| 카운트 플랏 sns.countplot |
 |
| sns.countplot( y='컬럼명', data= 데이터프레임) 범주값 몇 개 들어있는지 숫자 세기 |
|
 |
|
| sns.countplot( x='컬럼명', data= 데이터프레임) plt.grid() plt.show() |
|
| 기초 통계량 계산 0과 1 데이터 | 데이터프레임['컬럼명'].value_counts() 데이터프레임['컬럼명'].value_counts(normalize = True) |
| 시각화 - 파이차트 |  |
| plt.데이터프레임(컬럼명.values, labels = 컬럼명.index, autoptc='%.2%%', startangle = 90, counterclock = False, explode = [0.05, 0.05, 0.05], shadow =True) plt.show() |
이변량_숫자 vs 숫자
| 시각화 산점도 |  |
| sns.scatterplot( x = '컬럼명', y = '컬럼명', data = 데이터프레임 ) | |
| pairplot으로 한 번에 시각화 |  |
| sns.pairplot( 데이터프레임, kind = 'reg' ) | |
| jointplot |  |
| sns.pariplot( x='컬럼명', y= ' 컬럼명', data = 데이터프레임) | |
| regplot | 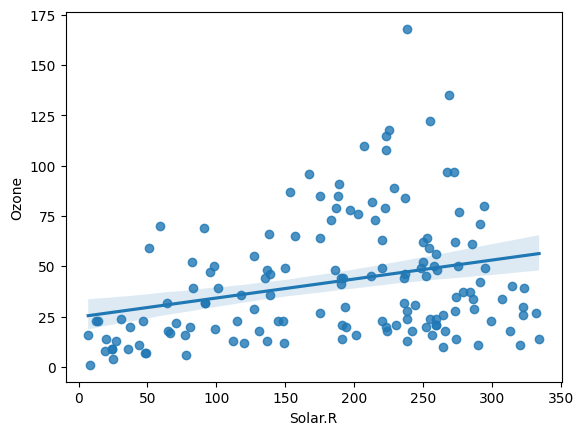 |
| sns.regplot(x='컬럼명', y = '컬럼명' , data = 데이터프레임) |
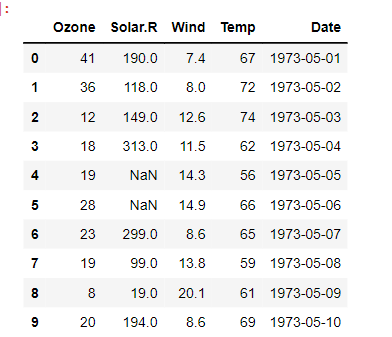
이변량_숫자 vs 숫자 -> 상관분석
| 패키지 | import scipy.stats as spst |
| 상관계수와 p-value | 계산 코 spst.pearsonr(데이터프레임['컬럼명'], 데이터프레임['컬럼명']) |
| 상관계수 구하기 | 데이터프레임.corr() |
| 상관계수 히트맵 시각화 |  |
| sns.heatplot( air.corr(), annot = True # 숫자(상관계수) 표기 여부 fmt = '.3f ' # 숫자 포맷 : 소수점 3자리까지 표기 cmap = 'RdYlBu_r' # 칼라맵 vmin = -1, vmax = 1) # 숫자(상관계수) 표기 여부 |
평균 개념
| 표준오차 SE Standard Error |
표준오차는 표준편차와 다른 개념 표본을 뽑아내어 모집단을 추정 표본 평균이 모평균과 완전히 일치할 수 없으며 이 오차를 '표준오차'라 한다. |
| 95% 신뢰구간 |  |
| sns.hisplot( 리스트, bins = 숫자) plt.axvline( np.mean(리스트), color = '색상' ) plt.text(np.mean(pop)=1, 30000, f' pop:mean : {np.mean(pop).round(3)}', color = 'r' ) plt.show() |
|
| errorbar |
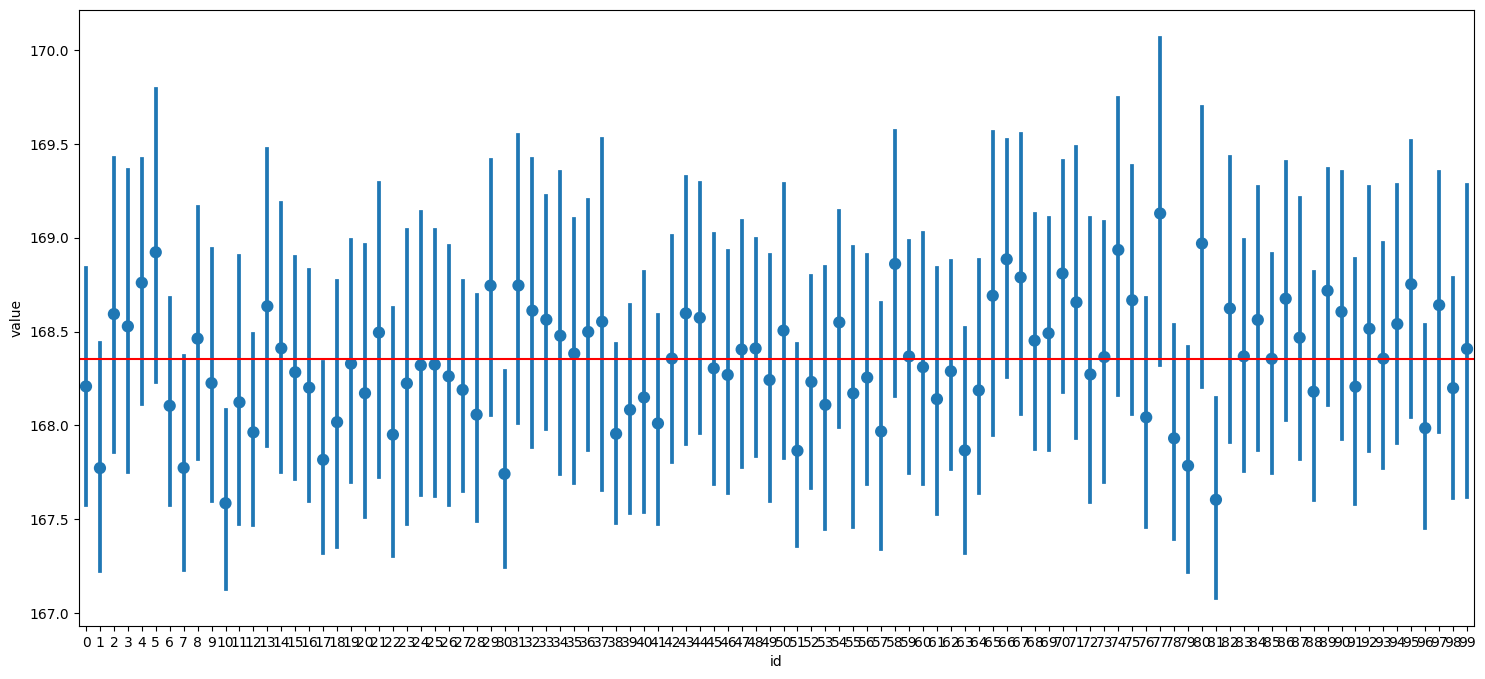 |
| # 100번 샘플링 samples = {'id' : [ ], 'value' : [ ]} for i in range(100) : samples['id'] += [i] * 100 samples['value'] += rd.sample(pop, 100) samples = pd.DataFrame(samples) samples.shape >> (10000, 2) 출력 sns.pointplot ( x = 'id' , y = 'value', data = samples, join = False) # join = False 독립적인 점들을 연결하지 않는다. plt.axhline(np.mean(pop), color, color = 'r') # pop이 모집단 plt.show() |
이변량_범주 vs 숫자
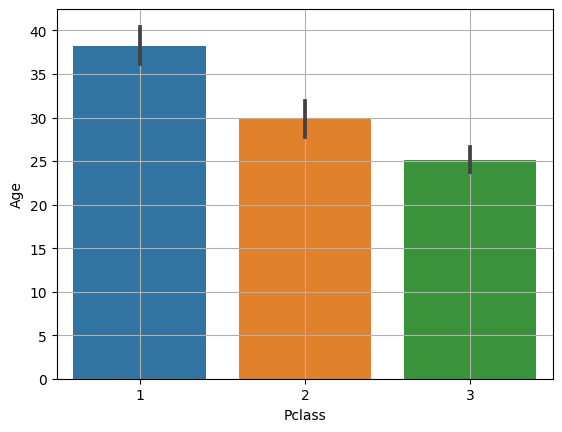
| 평균 비교 barplot |
 |
| sns.barplot( x= ' 컬럼명', y = '컬럼명', data = 데이터프레임 ) plt.grid() plt.show() sns.barplot( x='Survived', y = 'Age', data = titanic) 생존 여부에 따른 Age의 평균 비교 |
|
| boxplot | sns.boxplot( x='컬럼명', y='컬럼명', data = 데이터프레임 ) 실제코드 sns.boxplot( x= 'Survived', y = 'Age', data = titanic ) |
| NaN 결측치 제거 | 데이터프레임.loc [ 데이터프레임 ['컬럼명].notnull() ] |
| t-test | 실제 코드 temp = titanic.loc[titanic['Age'].notnull()] died = temp.loc[temp['Survived'] ==0, 'Age'] survived = temp.loc[temp['Survived'] ==1, 'Age'] spst.ttest_ind(died, survived) |
| 실제 코드 ( 성별에 대해 시행 ) male = titanic.loc[ titanic['Sex'] =='male', 'Fare' ] female = titanic.loc[ titanic['Sex'] =='female', 'Fare' ] spst.ttest_ind(male, female) |
|
| t-test를 통해 얻은 p-value 값이 0.05 보다 크다면 두 집단 간의 평균에 큰 차이가 없다는 귀무가설을 채택한다. 예시) t-통계량 2.067 ==> 2보다 크므로 차이가 있기는 있으나 크지는 않다. p-value : 0.039 ==> 0.05 보다 작으므로, 차이가 있기는 하지만 크지는 않다. |
|
| anova Analysis Of VAriance |
 |
| 여러 집단 간에 차이 비교 P_1 = temp.loc[ temp.Pclass ==1, 'Age'] P_2 = temp.loc[ temp.Pclass ==2, 'Age'] P_3 = temp.loc[ temp.Pclass ==3, 'Age'] spst.f_oneway( P_1, P_2, P_3 ) |
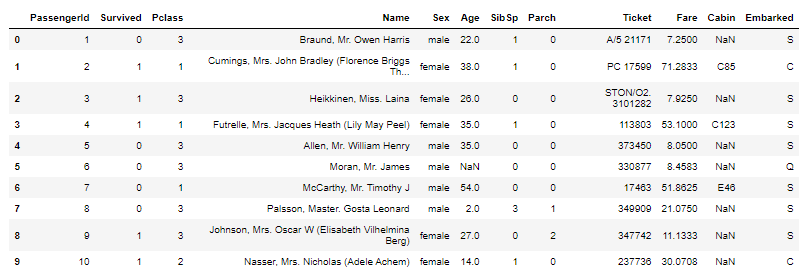
이변량 범주 vs 범주
| 교차표 pd.crosstab(행, 열) |
pd.crosstab(행, 열) pd.crosstab( 데이터프레임['컬럼명], 데이터프레임['컬럼명'], normalize = 'coulmns') >> normalize 옵션에는 columns, index, all 이 존재 |
| 시각화 mosaic |
 |
| mosaic( 데이터프레임, ['컬럼명', '컬럼명'] ) 실제 코드 mosaic( titanic, ['Pclass, 'Survived'] ) plt.axhline( 1- titanic['Survivde].mean(), color = 'r' ) plt.show() 모자이크에서 밑에가 사망이므로 1 - titanic['Survived']로 한다. |
|
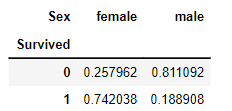
| 카이제곱 검정 | 범주형 변주들 사이에 어떤 관계가 있는지 수치화 spst.chi2_contingency(table) normalize를 하면 안된다. >> 두 개 이상의 범주형 변수 간에 독립성을 검정하는 데 사용한다 따라서, 검정을 통해 변수 간의 연관성을 파악하려면 원본 교차표를 사용해야 한다. Normalize하면 행과 열 합이 1이 되도록 스케일을 조정한다. 범주 간의 상대적 비율을 확인할 때는 유용하지만, 카이제곱 검정의 경우, 범주 간의 독립성을 여부를 확인하는 것이 목적이므로 스케일 조정을 하지 않는다. 카이제곱 검정 귀무가설 : 두 변수 간에 독립성이 있다. p-value가 0.05보다 클 때, 채택 대립가설 : 두 변수 간에 독립성이 없다. p-value가 0.05보다 작을 때, 채택 <주의> ttest 귀무가설 : 두 집단 간의 평균에 유의미한 차이가 없다. p-value가 0.05보다 클 때, 채택 대립가설 : 두 집단 간의 평균에 유의미한 차이가 있다. p-value가 0.05보다 작을 때, 채택 |
이변량 숫자 vs 범주
| 숫자 --> 범주 시각화 |
 |
| sns.histplot( x = '숫자 컬럼', data = 데이터프레임, hue ='범주 컬럼' ) | |
| kdeplot 작성 |
 |
| sns.kdeplot( x='숫자 컬럼', data= 데이터프레임, hue = '범주 컬럼' ) sns.kdeplot( x='숫자 컬럼', data = 데이터프레임, hue = '범주컬럼', common_norm = False ) >> common_norm = True가 기본 값 common을 붙였으므로 전체에 대한 비율을 요구한다. |