[통계 기초의 모든것 올인원] 메타코드 강의 후기 - "2강 확률과 확률변수"
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
조건부 확률

모집단의 20%가 A이므로, P(A) = 0.2로 설정하고, 이에 따라 나머지 집단인 B에 대해서는 P(B)로 설정하였습니다.
A 고객에 대하여 사고가 날 확률을 정의하면 P(C|A) = 0.3으로 계산할 수 있습니다.
B 고객에 대하여 사고가 날 확률을 정의하면 P(C|B) = 0.1로 계산할 수 있습니다.
조건부 확률에 대한 식을 생각하면, P(C∩B) / P(B) 이므로 P(C∩B) 값을 구할 수 있고 A에 대해서도 같은 과정을 수행할 수 있습니다. 따라서 구한 값들을 더한다면 새 고객에 대한 사고 확률을 계산할 수 있습니다.
베이즈 정리

사전 확률을 사후 확률로 전환할 수 있다는 것이 베이즈 정리에서의 가장 중요한 점입니다.
데이터가 추가됨에 따라 확률을 업데이트 할 수 있습니다.
예시로서, 성적이 얼마나 오를지에 대해 예측하는 것을 들어주셨습니다.
대상에 대하여, "책을 몇 개 샀다", "이번 모의고사에서 몇 점 맞았다"의 정보가 추가됨에 따라 사후 확률을 추정할 수 있게됩니다.
확률변수

확률 변수는 이름은 변수로 되어있지만, 함수를 의미합니다.
사건의 실수값을 맵핑하는 개념으로 생각하면 된다고 설명을 해주셨습니다.
확률분포는 확률변수를 설명해주는 개념입니다.
밑의 예시를 통하여 보다 확률 변수를 쉽게 이해할 수 있도록 돕는 것입니다.
이산확률변수, 연속확률변수

이산확률의 경우 정의된 확률의 값을 셀 수 있습니다.
따라서 확률질량 함수의 경우 특정 값에 대해 각 확률이 대응됩니다.
연속확률 변수의 경우 이산확률변수와는 다르게, 특정 값으로 정해지지 않는다는 특성을 갖습니다.
연속형이므로, 취할 수 있는 값이 무한대에 해당한다는 특징이 있습니다.
기대값 - 이산확률변수, 연속확률변수

이산확률 변수의 경우, 각 변수에 대하여 일어날 확률을 곱하는 과정을 수행합니다.
이후에 해당 값들을 모두 더해주면 이산확률변수에서의 기대값인 E(X) 값을 계산할 수 있습니다.
연속확률 변수의 경우, 위에서와 마찬가지로 변수에 확률을 곱하는 과정을 수행합니다.
연속형 값이므로 더해주는 것이 아닌 적분을 수행한다는 것이 위의 과정과 차이가 있습니다.
기대값에 대한 공식
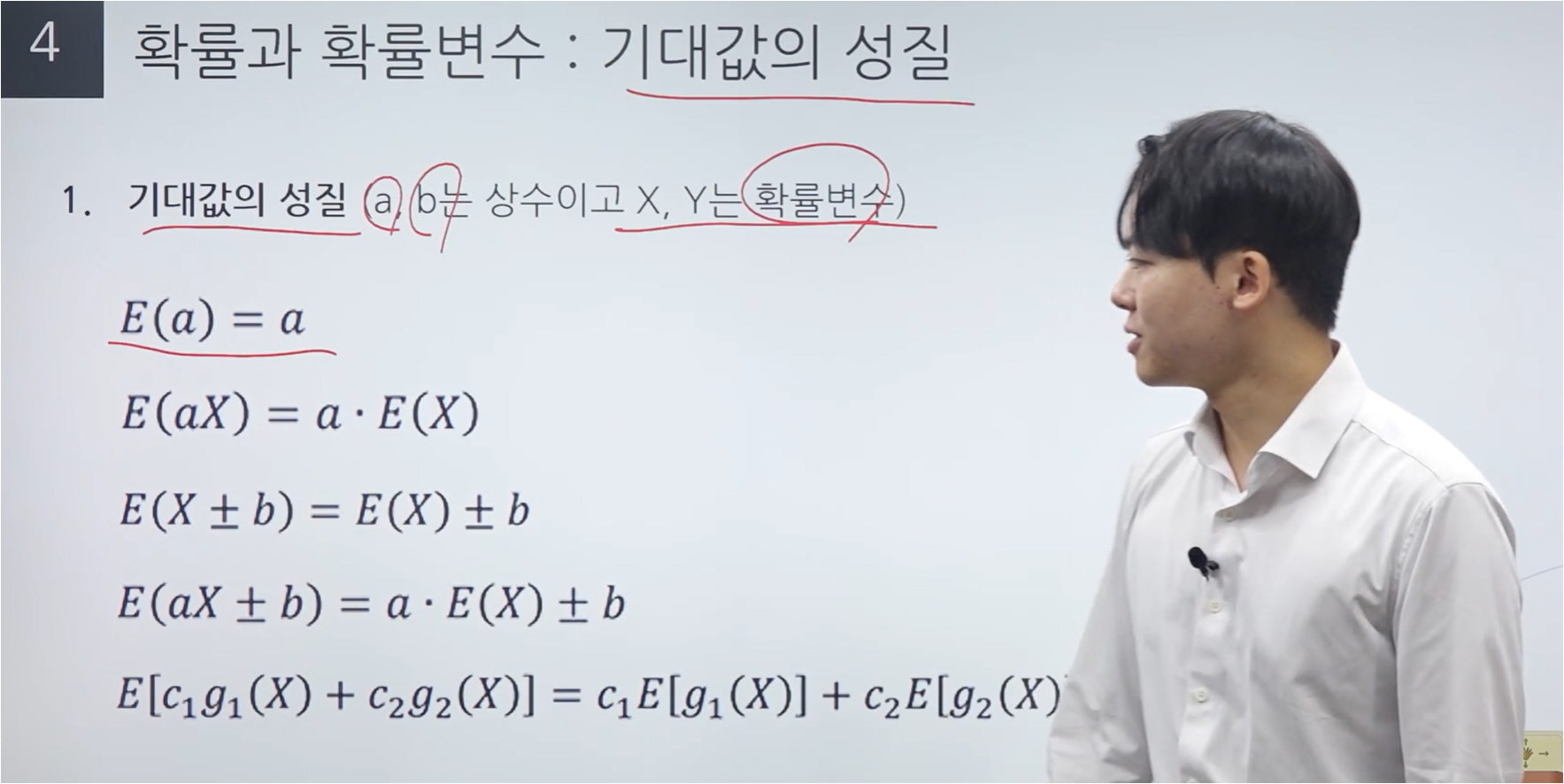
위 식들은 기대값에 대하여 외워두면 좋은 공식들입니다.
가장 위의 E(a)의 경우 상수 a에 대한 기대값은 상수 a라는 것을 의미합니다.
E(X + b)의 경우, 우리나라 선수들의 평균 키보다 A 국가대표팀들의 평균 키가 3cm 큰 상황을 예시로 들어주셨습니다.
이 경우 A 국가대표팀에 대하여 평균을 구하는 것이 아닌 우리나라 선수들의 평균 키에서 3cm를 더하면 됩니다.
'통계 - 메타코드' 카테고리의 다른 글
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 통계적 추정 (1) | 2024.05.19 |
|---|---|
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 연속확률분포, 통계적 추정 (0) | 2024.05.19 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 연속확률분포 (0) | 2024.05.12 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 이산확률분포 (0) | 2024.05.12 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - "1강 통계량" (0) | 2024.05.04 |