[통계 기초의 모든것 올인원] 메타코드 강의 후기 - 대응비교, 모비율, 모분산 비교
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
대응비교

paired t-test, 같은 개체에 대하여 실험 전후 값을 측정한다.
따라서 독립이라고 보기는 어렵다. ⇒ 독립 가정이 빠진다.
대응표본은 독립이 아닌 것을 말하며, 이들을 통해 비교를 수행하는 것이 대응비교의 개념이다.
모표분편차가 들어가지 않기 때문에 표본 표분편차를 사용하고 t 분포를 따르는 통계량을 사용한다.
두 모비율 비교

Variance는 독립이라면 괄호 안이 각각 더하기로 나누어질 수 있다.
표본의 크기가 큰 경우에 대한 수식은, Variance에 대해 식을 나누는 과정을 수행하고 각각에 대한 Var 값을 대입한 것이다.
마지막 식에서 분모 부분이 복잡하게 보이지만 단순하게 위에서의 Var 값을 대입한 것 뿐이다.
최종적으로는 표준정규분포를 따르게 됨을 말하며 따라서 Z 통계량을 사용한다.
두 모비율 비교

( 알파 / 2 ) 쓰여 있음을 통해 양측검정을 수행함을 알 수 있다.
“1. p1 - p2 신뢰구간” 수식에서 루트 안에 있는 값은 앞 슬라이드에서의 Variance에 해당하며, 두 집단이 독립이기 때문에 각각의 Variance를 더하기로 나눈 것이다.
“2. 표본의 크기가 큰 경우” 수식에서 귀무가설이 맞다면 기댓값 E는 당연하게 0이 된다.
공동 모비율 p의 합동 추정량 식은, 합동이라는 개념이므로 분자와 분모에 각각에 대한 합의 값이 적혀있다고 우선 받아들인다.
예시 문제

강의 A를 듣고 시험을 본 경우와 강의 B를 듣고 시험을 본 경우를 비교한 것이다.
강의 A의 합격률은 0.7, 강의 B의 경우 합격률은 0.6이 된다.
95%에 대한 신뢰 구간이므로 알파는 1-0.95 = 0.05가 된다.
양측 검정이므로 알파 = 0.025일 때의 Z 통계량 값은 1.96이 된다.
우측은 Standard Error 수식이다.
예시 문제 2

강의 A를 수강한 학생이 합격률이 더 높은지 확인하고 싶으므로, 귀무가설은 두 집단의 합격률이 같다가 된다.
합동추정량 계산에서 분모에는 각각의 표본의 숫자를 더하므로 100 + 150이 된다.
합격자에 대해서도 70 + 90이 된다.
위에서 구한 값들에 따라 계산을 진행하면 값은 1.6137이 된다.
모분산 비교
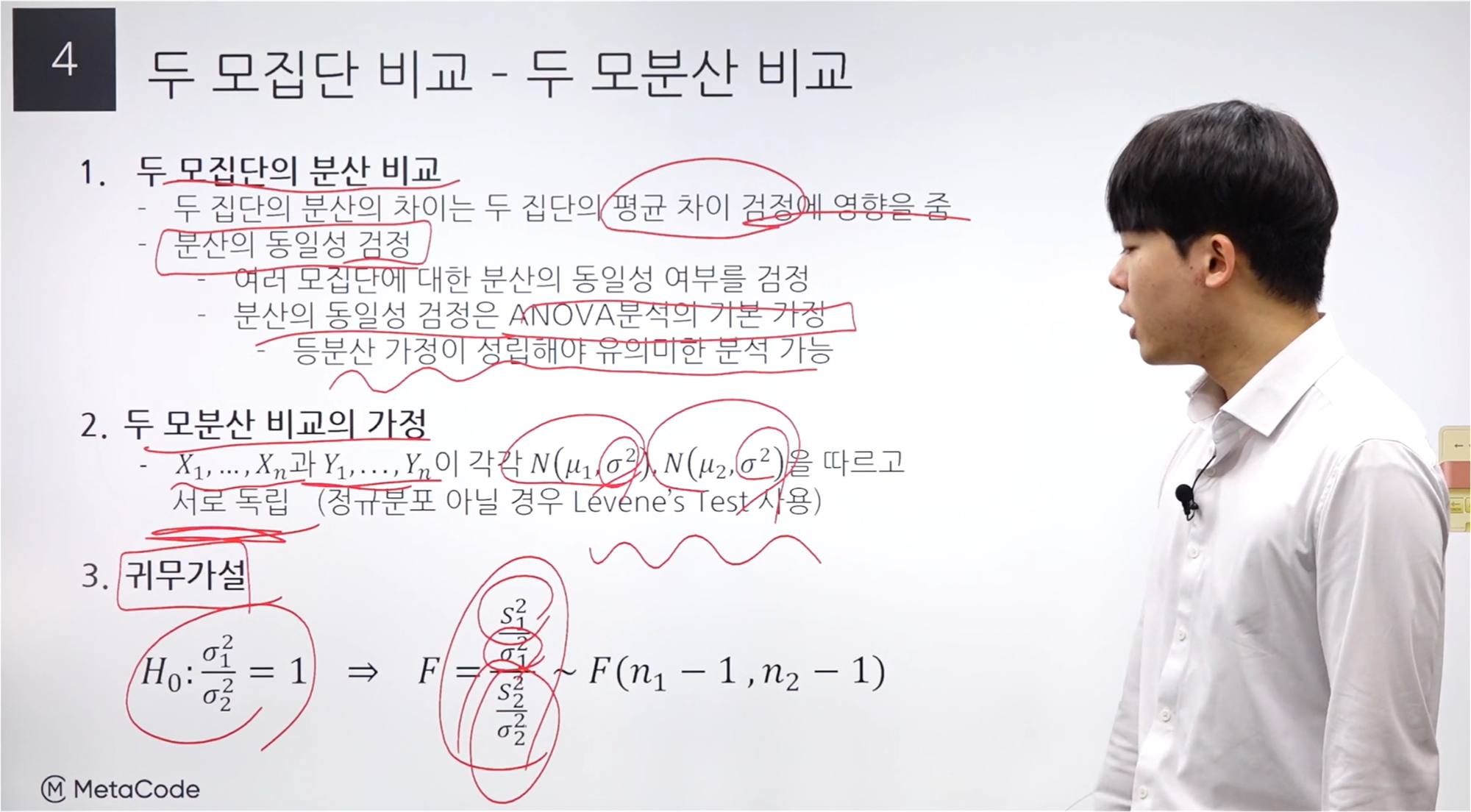
등분산 가정은 집단 간의 검정에 중요한 가정이 된다.
“2. 두 모분산 비교의 가정” 식에서 각각의 정규분포에 대해 시그마 값이 같게 되어 있고 서로 독립이라는 조건이 있으며,
이 경우에는 Levene’s Test를 사용한다고 되어 있다.
귀무가설은 두 모분산이 비율이 1이 된다(=같다)이다.
'통계 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 이원배치 분산분석_240623 (0) | 2024.06.23 |
|---|---|
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 일원분산분석_240623 (0) | 2024.06.23 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 모분산, 두 집단 비교_240616 (1) | 2024.06.16 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 검정 (0) | 2024.05.30 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 구간추정/표본크기결정, 검정 (0) | 2024.05.29 |