[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "기초수학 ~ 최소제곱법"
머신러닝 입문 부트캠프ㅣKAIST AI 박사과정
www.metacodes.co.kr
안녕하세요 메타코드 서포터즈 5기 송주영입니다.
인공지능을 코드로 먼저 접해서 이해도가 높지 않은 상태였는데, 이러한 강의를 찾게 되어서 만족스럽네요ㅎ
이 강의를 끝까지 수강하고 이론과 코딩 역량을 발전시키자는 계획을 세웠어요
강의 리뷰 시작하겠습니다!
이진분류, 다중분류

이진 분류와 다중 분류 문제에서 사용하는 시그모이드와 소프트 맥스 함수입니다.
시그모이드 함수의 경우 0.5를 기준으로 하여 이 값보다 높으면 1, 작으면 0으로 클래스를 두 가지로 분류합니다.
소프트맥스 함수는 다중 분류 문제를 위한 함수로, 시그마가 사용된 모습을 보입니다.
각각의 클래스에 대한 확률값을 반환합니다.
로그 함수

로그 함수는 지수 함수와 y = x 선을 기준으로 대칭이 되는 모습을 보입니다.
지수 함수와 역함수의 관계임을 의미합니다.
로그 함수의 밑이 e 일 때는 loge로 표현하기 보다는 ln으로 표현합니다.
표현은 자연로그라고 합니다.
선형 회귀

선형 회귀는 단순 선형 회귀, 다중 선형 회귀, 다항 회귀로 구분됩니다.
피처의 종류가 1개이면 단순 선형 회기입니다.
피쳐의 종류가 여러 개이면 다중 선형 회귀입니다.
독립 변수의 차수를 높이면 다항 회귀에 해당하고 수식에서 보면 x의 차수가 다름을 확인할 수 있습니다.
최적의 파라미터

Parameter란 모델이 데이터로부터 학습한 가중치를 말합니다.
최적이라는 표현은 데이터를 가장 잘 표현한다는 의미이며 이는 실제값과 예측값과의 차이가 적다는 것을 의미합니다.
즉, 손실이 가장 적게 일어나야 합니다.
정리하면 최적의 파라미터란 손실 함수값이 최소가 되는 경우의 모델 파라미터를 말합니다.
파라미터

Parameter의 종류에는 모델이 학습한 Parameter(=weight)와 사람이 설정하는 Hypeparameter가 있습니다.
Weight는 모델이 데이터로부터 직접 학습한 것으로 사람이 직접 개입하여 변경시키는 못합니다.
Hyperparameter에는 학습률, 배치 크기 등이 존재하며 이들의 적절한 값을 찾아 모델의 설명력을 높여야 합니다.
각각의 개념은 뒤의 강의에서 학습할 예정입니다.
회귀식 계산
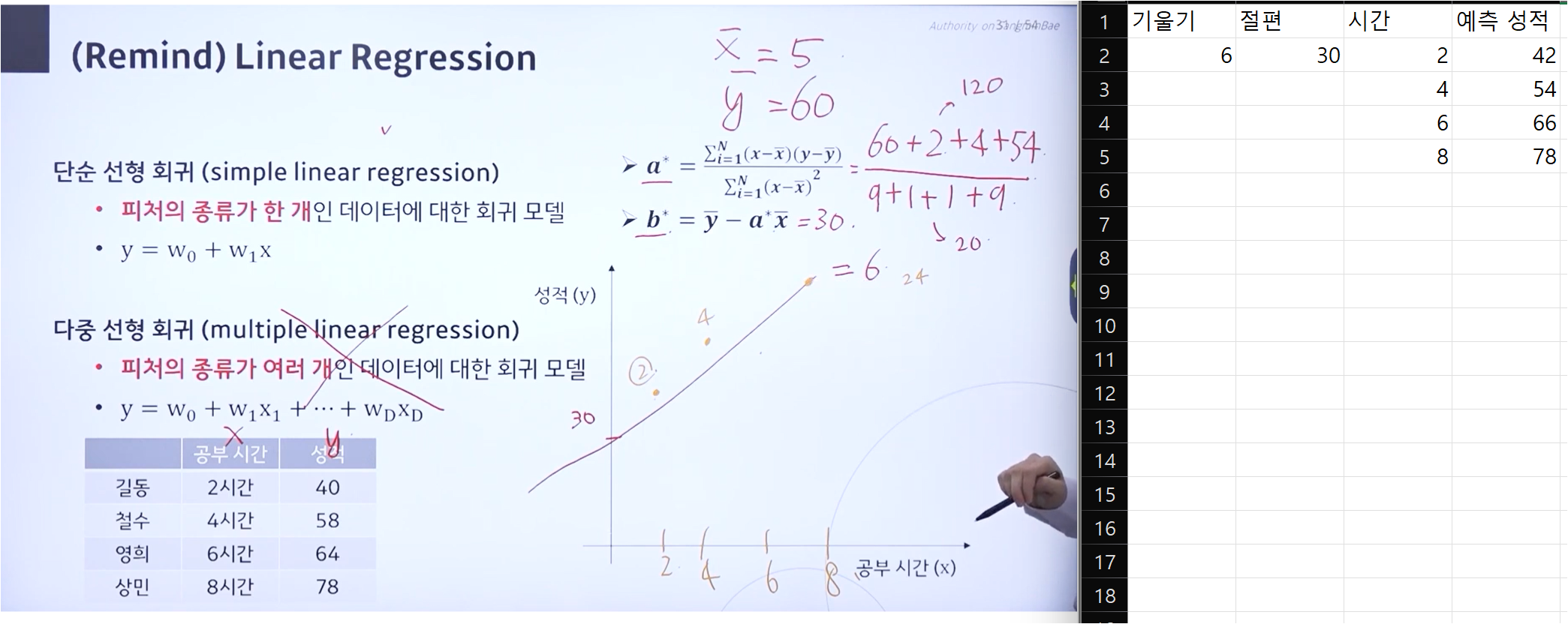
a∗는 기울기, b∗는 절편에 해당한다.
표를 기준으로 먼저 ¯x와 ¯y를 계산한다.
계산된 기울기와 절편값을 활용하여 예측값을 구한다.
공부 시간이 8시간일 때는 일치함을 확인할 수 있다.
산출된 식에 대해서 엑셀을 활용하여 결과값을 계산해보고, 실제값과의 차이를 계산해보니 흥미로웠습니다.
그동안 단순하게 코드를 입력하여 나온 결과값들을 사용하다가, 이번에는 직접 계산을 해보니 이해도를 높일 수 있었습니다.
읽어주셔서 감사합니다!!
'인공지능 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "1단원 실습" (0) | 2024.07.28 |
|---|---|
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Validation Data" (0) | 2024.07.27 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Bias and variance Trade-off" (0) | 2024.07.21 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Gradient Descent" (3) | 2024.07.20 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "강좌 소개 ~ 기초 수학" (1) | 2024.07.14 |