[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Validation Data"
머신러닝 입문 부트캠프ㅣKAIST AI 박사과정
www.metacodes.co.kr
안녕하세요 메타코드 서포터즈 5기 송주영입니다.
요즘 날씨가 변덕이 심해서, 나갈 때 항상 작은 우산을 휴대해서 나가고 있네요
다들 몸조리 잘하시길 바랄게요!!
공부하려면 컨디션을 잘 관리하는 것도 필수적이라 느끼고 있어요
강의 리뷰 시작하겠습니다!!
Validation Data

하나의 데이터셋을 받는다면, 이를 Train, Valid, Test Data로 나눕니다.
데이터셋을 나누는 목적은 Overfitting Issue를 막기 위함입니다.
Valid Data와 Test Data는 둘다 학습된 모델의 성능을 평가할 때 사용되기 때문에 헷갈릴 수 있습니다.
이 둘의 차이는 학습 과정에 참여하는 지의 여부입니다.
Valid Data는 학습 중간에 검증용으로 사용하며, 모델의 적절한 파라미터를 찾을 때 활용됩니다.
Test Data는 최종 학습이 완료된 모델의 성능을 평가할 때 사용합니다.
LOOCV and K-fold cross validation

하나의 데이터셋에 대해서만 검증을 할 경우에는, 보편적으로 높은 성능을 나타내는 모델을 찾는 데에 어려움을 겪을 수 있습니다.
이를 위해 사용하는 것이 LOOCV 방법입니다.
모든 데이터 샘플에 대하여 검증을 하는 것이 목적이며, 이 경우에는 계산 비용이 매우 큰 단점을 갖습니다.
이를 보완하기 위해 고안된 방법이 K-fold cross validation입니다.
K개의 파트로 데이터를 나누어 학습, 검증을 진행하여 적절한 계산 비용 내에서 높은 성능의 모델을 찾는 것이 목적입니다.
Regularization

모델의 파라미터 숫자가 많아지면, 모델의 복잡도가 커지게 됩니다.
모델의 복잡도가 커진다면 Bias Error는 줄어들지만, 과적합이 발생하는 문제가 생깁니다.
따라서, 정규화를 통해 중요한 파라미터만 선택하고 모델의 복잡도를 줄입니다.
정규화의 종류에는 Ridge 회귀와 Lasso 회귀가 존재합니다.
Ridge Regression

Ride Regression은 제곱합을 활용합니다.
빨간색 원은 β 값이 존재할 MSE 값을 표현하고, 중심에서 멀어질수록 Error가 커집니다.
빨간색 원과 파란색 원이 만난 지점이 MSE 값을 최소로 하는 지점입니다.
λ 값을 조절하여 β를 남길 지 버릴지 선택합니다.
Lasso Regression
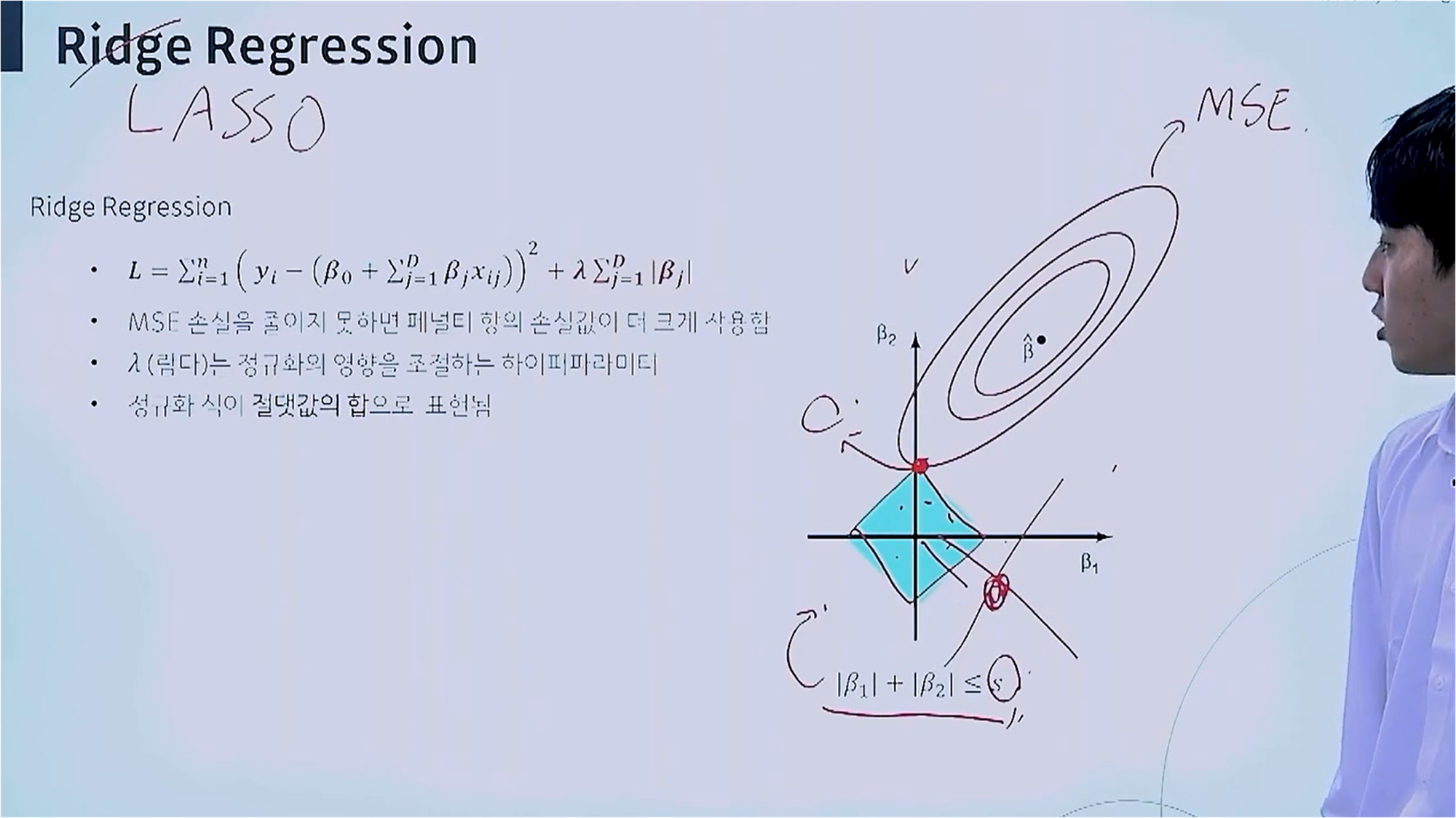
Lasso Regression에 대한 개념입니다.
Lasso Regression은 계수값이 0에 가까운지 여부를 확인하기 위해 정규화 식에 절댓값을 사용하며, 이는 Ridge Regression이 계수의 제곱을 사용하는 것과 차이점을 갖습니다.
Lasso Regression은 절댓값을 사용하므로, 마름모 형태를 보입니다.
빨간색 원과 맞닿은 지점에서 β1은 값이 존재하지 않기 때문에, 적절한 λ 값을 선택함으로써, β1이 0에 가깝게 되도록 합니다.
파라미터 간소화

Lasso가 파라미터 갯수를 줄이는 데에 더 효과적인 모습을 보입니다.
파라미터 갯수를 줄이는 방법에는 λ 값을 키우는 것과 지수 값을 낮추는 방법이 존재합니다.
λ 값을 키우면 βi 값은 그만큼 작아지게 됩나다.
지수를 줄이는 경우, 마름모 그림이 더욱 움푹 패인 형태가 되어 βi 값을 최소로 하는 지점과 원이 맞닿게 됩니다.
이상으로 강의 리뷰 마치겠습니다!!
글 읽어주셔서 감사합니다

'인공지능 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Logistic Regression" (0) | 2024.07.30 |
|---|---|
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "1단원 실습" (0) | 2024.07.28 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Bias and variance Trade-off" (0) | 2024.07.21 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Gradient Descent" (3) | 2024.07.20 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "기초수학 ~ 최소제곱법" (3) | 2024.07.14 |