하나둘셋넷

[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "1단원 실습"

메타코드M (metacodes.co.kr)

안녕하세요 메타코드 서포터즈 5기 송주영입니다.

드디어 1단원 이론 수업을 마치고, 코딩 실습을 하게 되었습니다.

실습을 하면서 이론 때 배워둔 내용을 더 확실하게! 이해하는 게 목표에요

인공지능 혹은 코딩 관련 분야에 관심을 갖고 계신다면 "이론 공부 and 코딩 실습" 루틴으로 공부를 하는 게 좋을 거 같아요

강의 리뷰 시작하겠습니다.

실습 환경 - Colab

코딩 실습은 Colab 환경에서 진행되었습니다.

Colab은 구글에서 제공하는 온라인 코딩 환경입니다.

Python 언어를 Jupyter 환경에서 제공하여 마크다운 셀을 통해 편리하게 필기할 수 있다는 장점을 갖습니다.

다만, 세션 유지 시간이 정해져 있어서 이 부분을 염두에 둘 필요가 존재합니다.

드라이브 연결

구글 드라이브와 Colab을 연결하는 코드입니다.

해당 코드를 입력하면 연결을 할 것인지 묻는 창이 나오며 동의를 클릭하면 연결이 완료됩니다.

ls 명령어를 통해 현재 디렉토리의 파일을 확인할 수 있습니다.

cd 명령어를 통해 디렉토리의 위치를 변경할 수 있습니다.

학습 데이터와 평가 데이터로 나누기

sklearn을 통하여 데이터를 학습용과 평가용으로 나누었습니다.

test_size를 통해 학습용과 평가용의 비중을 어떻게 할 지 설정합니다. 이 경우에는 90:10 비율로 설정했습니다.

random_state를 통해서는 seed 값을 고정하여 항상 동일한 데이터가 추출되도록 합니다.

나눈 데이터는 X_train, X_test, y_train, y_test 변수에 할당됩니다.

경사하강법

경사 하강법을 활용하여 학습을 진행하는 모습입니다.

loss 변수에 MSE 손실함수 식을 할당했고, numpy의 mean 함수를 활용했습니다.

Gradient 계산을 위한 편미분 값도 dw, db 변수에 할당했고, 아래 줄에서는 w와 b 변수가 업데이트가 됩니다.

lr은 learning_rate입니다.

weights와 bias 값은 리스트에 append 되고 최종적으로는 w, b, w_list, b_list, loss_list의 5개의 변수가 반환됩니다.

LinearRegression 모델 활용, 최소 제곱법(Least Squares Method)

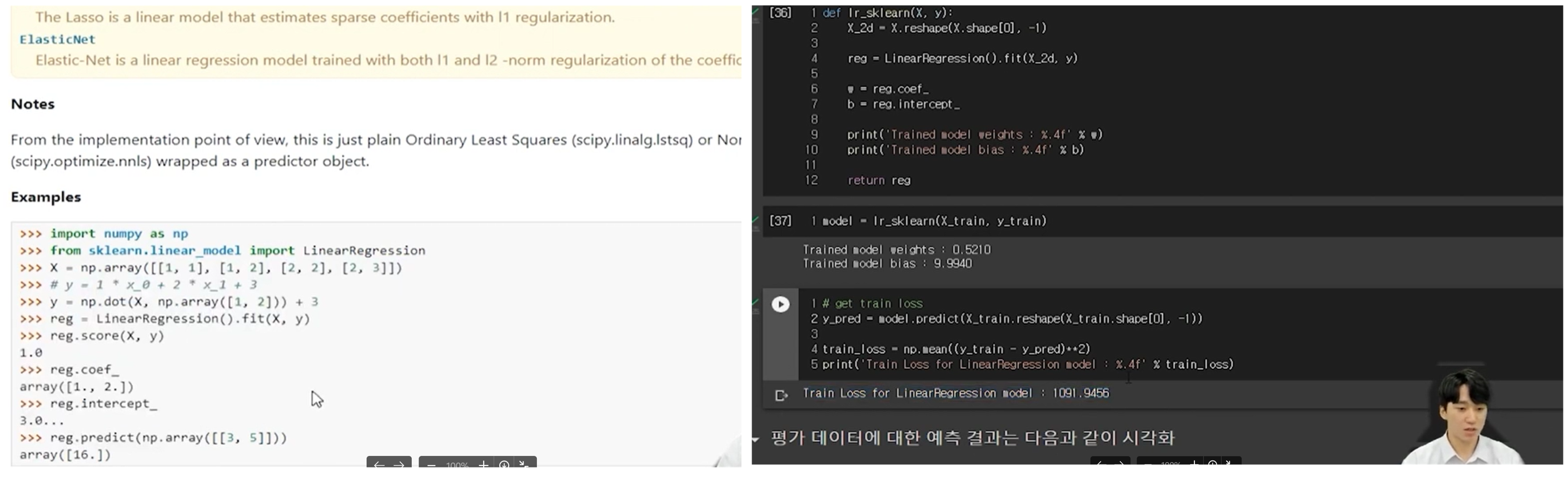
sklearn 라이브러리의 LinearRegression 모델을 활용하여 모델을 학습하는 코드입니다.

해당 모듈은 경사하강법 대신에 최소 제곱법을 사용해 모델을 학습합니다.

reshape 메서드를 통해 데이터를 알맞은 형태로 변형하였습니다.

y_pred에 예측값을 저장하고, 이를 통해 train_loss 값을 계산했습니다.

predict() 메서드는 x를 통해 예측을 수행하는 것으로, x 인자만 필요하고 y 인자는 필요로 하지 않습니다.

SGDRegressor

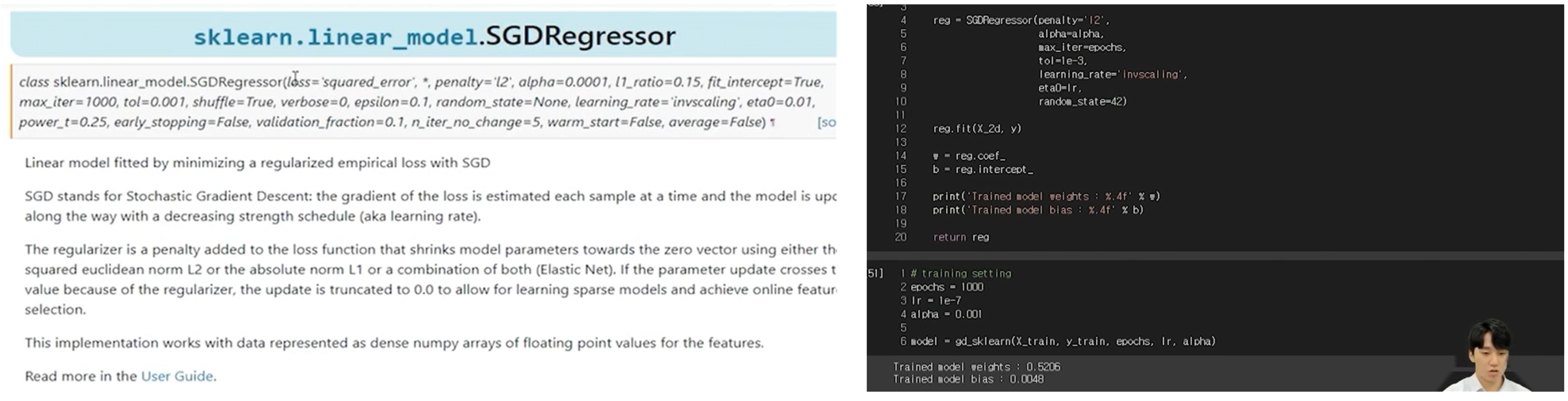
마지막으로 SGDRegressor를 통한 모델 학습입니다.

tol 값을 설정하면 loss 값이 특정 값에 도달하였을 때 학습이 중단되게 할 수 있습니다.

경사하강법, LinearRegerssion, SGDRegressor를 통해 모델을 학습하는 방법을 배웠습니다.

train_loss = np.mean((y_train-y_pred)**2)

코드를 통하여 MSE 값을 비교하며 어떤 모델이 가장 학습이 잘 되는지 확인할 수 있습니다.

확인 결과는 LinearRegression을 통해 최소제곱법을 사용했을 때가 가장 높은 성능을 보였습니다.

[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Validation Data"

메타코드M (metacodes.co.kr)

안녕하세요 메타코드 서포터즈 5기 송주영입니다.

요즘 날씨가 변덕이 심해서, 나갈 때 항상 작은 우산을 휴대해서 나가고 있네요

다들 몸조리 잘하시길 바랄게요!!

공부하려면 컨디션을 잘 관리하는 것도 필수적이라 느끼고 있어요

강의 리뷰 시작하겠습니다!!

Validation Data

하나의 데이터셋을 받는다면, 이를 Train, Valid, Test Data로 나눕니다.

데이터셋을 나누는 목적은 Overfitting Issue를 막기 위함입니다.

Valid Data와 Test Data는 둘다 학습된 모델의 성능을 평가할 때 사용되기 때문에 헷갈릴 수 있습니다.

이 둘의 차이는 학습 과정에 참여하는 지의 여부입니다.

Valid Data는 학습 중간에 검증용으로 사용하며, 모델의 적절한 파라미터를 찾을 때 활용됩니다.

Test Data는 최종 학습이 완료된 모델의 성능을 평가할 때 사용합니다.

LOOCV and K-fold cross validation

하나의 데이터셋에 대해서만 검증을 할 경우에는, 보편적으로 높은 성능을 나타내는 모델을 찾는 데에 어려움을 겪을 수 있습니다.

이를 위해 사용하는 것이 LOOCV 방법입니다.

모든 데이터 샘플에 대하여 검증을 하는 것이 목적이며, 이 경우에는 계산 비용이 매우 큰 단점을 갖습니다.

이를 보완하기 위해 고안된 방법이 K-fold cross validation입니다.

K개의 파트로 데이터를 나누어 학습, 검증을 진행하여 적절한 계산 비용 내에서 높은 성능의 모델을 찾는 것이 목적입니다.

Regularization

모델의 파라미터 숫자가 많아지면, 모델의 복잡도가 커지게 됩니다.

모델의 복잡도가 커진다면 Bias Error는 줄어들지만, 과적합이 발생하는 문제가 생깁니다.

따라서, 정규화를 통해 중요한 파라미터만 선택하고 모델의 복잡도를 줄입니다.

정규화의 종류에는 Ridge 회귀와 Lasso 회귀가 존재합니다.

Ridge Regression

Ride Regression은 제곱합을 활용합니다.

빨간색 원은 $\beta $ 값이 존재할  MSE 값을 표현하고, 중심에서 멀어질수록 Error가 커집니다.

빨간색 원과 파란색 원이 만난 지점이 MSE 값을 최소로 하는 지점입니다.

$\lambda $ 값을 조절하여 $\beta $를 남길 지 버릴지 선택합니다.

Lasso Regression

Lasso Regression에 대한 개념입니다.

Lasso Regression은 계수값이 0에 가까운지 여부를 확인하기 위해 정규화 식에 절댓값을 사용하며, 이는 Ridge Regression이 계수의 제곱을 사용하는 것과 차이점을 갖습니다.

Lasso Regression은 절댓값을 사용하므로, 마름모 형태를 보입니다.

빨간색 원과 맞닿은 지점에서 $\beta_{1}$은 값이 존재하지 않기 때문에, 적절한 $\lambda $ 값을 선택함으로써, $\beta_{1}$이 0에 가깝게 되도록 합니다.

파라미터 간소화

Lasso가 파라미터 갯수를 줄이는 데에 더 효과적인 모습을 보입니다.

파라미터 갯수를 줄이는 방법에는 $\lambda $ 값을 키우는 것과 지수 값을 낮추는 방법이 존재합니다.

$\lambda $ 값을 키우면 $\beta_{i}$ 값은 그만큼 작아지게 됩나다.

지수를 줄이는 경우, 마름모 그림이 더욱 움푹 패인 형태가 되어 $\beta_{i}$ 값을 최소로 하는 지점과 원이 맞닿게 됩니다.

이상으로 강의 리뷰 마치겠습니다!!

글 읽어주셔서 감사합니다

[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "기초수학 ~ 최소제곱법"

메타코드M (metacodes.co.kr)

안녕하세요 메타코드 서포터즈 5기 송주영입니다.

인공지능을 코드로 먼저 접해서 이해도가 높지 않은 상태였는데, 이러한 강의를 찾게 되어서 만족스럽네요ㅎ

이 강의를 끝까지 수강하고 이론과 코딩 역량을 발전시키자는 계획을 세웠어요

강의 리뷰 시작하겠습니다!

이진분류, 다중분류

이진 분류와 다중 분류 문제에서 사용하는 시그모이드와 소프트 맥스 함수입니다.

시그모이드 함수의 경우 0.5를 기준으로 하여 이 값보다 높으면 1, 작으면 0으로 클래스를 두 가지로 분류합니다.

소프트맥스 함수는 다중 분류 문제를 위한 함수로, 시그마가 사용된 모습을 보입니다.

각각의 클래스에 대한 확률값을 반환합니다.

로그 함수

로그 함수는 지수 함수와 y = x 선을 기준으로 대칭이 되는 모습을 보입니다.

지수 함수와 역함수의 관계임을 의미합니다.

로그 함수의 밑이 e 일 때는 $log_{e}$로 표현하기 보다는 $ln$으로 표현합니다.

표현은 자연로그라고 합니다.

선형 회귀

선형 회귀는 단순 선형 회귀, 다중 선형 회귀, 다항 회귀로 구분됩니다.

피처의 종류가 1개이면 단순 선형 회기입니다.

피쳐의 종류가 여러 개이면 다중 선형 회귀입니다.

독립 변수의 차수를 높이면 다항 회귀에 해당하고 수식에서 보면 x의 차수가 다름을 확인할 수 있습니다.

최적의 파라미터

Parameter란 모델이 데이터로부터 학습한 가중치를 말합니다.

최적이라는 표현은 데이터를 가장 잘 표현한다는 의미이며 이는 실제값과 예측값과의 차이가 적다는 것을 의미합니다.

즉, 손실이 가장 적게 일어나야 합니다.

정리하면 최적의 파라미터란 손실 함수값이 최소가 되는 경우의 모델 파라미터를 말합니다.

파라미터

Parameter의 종류에는 모델이 학습한 Parameter(=weight)와 사람이 설정하는 Hypeparameter가 있습니다.

Weight는 모델이 데이터로부터 직접 학습한 것으로 사람이 직접 개입하여 변경시키는 못합니다.

Hyperparameter에는 학습률, 배치 크기 등이 존재하며 이들의 적절한 값을 찾아 모델의 설명력을 높여야 합니다.

각각의 개념은 뒤의 강의에서 학습할 예정입니다.

회귀식 계산

$ {a}^*$는 기울기, $ {b}^*$는 절편에 해당한다.

표를 기준으로 먼저 $\overline{x}$와 $\overline{y}$를 계산한다.

계산된 기울기와 절편값을 활용하여 예측값을 구한다.

공부 시간이 8시간일 때는 일치함을 확인할 수 있다.

산출된 식에 대해서 엑셀을 활용하여 결과값을 계산해보고, 실제값과의 차이를 계산해보니 흥미로웠습니다.

그동안 단순하게 코드를 입력하여 나온 결과값들을 사용하다가, 이번에는 직접 계산을 해보니 이해도를 높일 수 있었습니다.

읽어주셔서 감사합니다!!