[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Bias and variance Trade-off"
머신러닝 입문 부트캠프ㅣKAIST AI 박사과정
www.metacodes.co.kr
안녕하세요 메타코드 서포터즈 5기 송주영입니다.
머신러닝을 공부함에 있어서 코딩으로 넘어가기 전에 기초 이론을 다지는 이 부분이 쉽게 않게 느껴지네요.
통계학과나 수학과 분들이 부러워지는 순간이었어요
그래도 힘내서 끝까지 완주해보겠습니다!
Training Data vs Test Data

데이터를 받게 된다면 하나의 데이터셋을 통째로 받게 됩니다.
이 데이터셋에 대해 일정 퍼센티지에 따라서 학습용으로 사용할 데이터와 평가용으로 사용할 데이터로 나눕니다.
데이터를 나누는 과정에서는 랜덤 샘플링 과정을 수행합니다.
보통 학습용으로 80%를 정하고 20%를 평가 데이터로 할당합니다.
모델의 복잡도

모델의 복잡도는 선형에서 비선형으로 갈수록 더 올라갑니다.
선형 함수는 단순히 기울기와 절편으로 이루어져 있고, 차수가 올라갈수록 파라미터가 하나씩 증가하는 것을 생각해보면 당연합니다.
모델이 복잡해질수록 학습 데이터를 잘 학습한다는 장점을 갖습니다.
대신, 모델이 복잡한데 데이터가 모자르다면 충분한 학습이 이루어지 지지 않는 Under-fitting 현상이 발생하기 때문에 무조건 좋은 것은 아닙니다.
편향과 분산 - (1)

편향과 분산은 모두 알고리즘이 가지고 있는 에러의 종류로서 이들을 합친 것이 MSE 값입니다.
평균에 대한 분배 법칙을 따라서 해당 수식을 전개하는 과정입니다.
θ는 우리가 모르는 어떤 특정값을 말합니다. 따라서 정해진 값이기 때문에 랜덤성, 평균이 없습니다.
따라서 수식에서 3번째 항은 그대로 나온 모습을 보입니다.
편향과 분산 - (2)

편향은 실제값과 예측값의 차이를 말합니다.
이는 학습 데이터에 대한 정확도라고 이해할 수도 있습니다.
분산은 예측값의 범위를 말합니다. 따라서 분산이 크다면 첫 번째 예측값과 두 번째 예측값이 크게 달라지게 됩니다.
분산이 적다면 여러 번 추정을 하더라도 비슷한 값을 가지게 될 것이다.
편향과 분산 - (3)

편향은 정답과 예측값의 차이를 말합니다.
이 그림에서는 빨간색 점을 정답, 파란색 점은 예측으로 표현했습니다.
Low Variance 상태를 보면 파란색 점들이 뭉쳐 있는 모습을 보이고, Low Bias일 때는 빨간색 점과 파란색 점과의 거리가 좁은 모습을 보입니다.
즉 Variance는 정답 여부를 떠나서, 얼마나 일정한 값을 도출하는가를 말합니다.
편향과 분산 - (3)
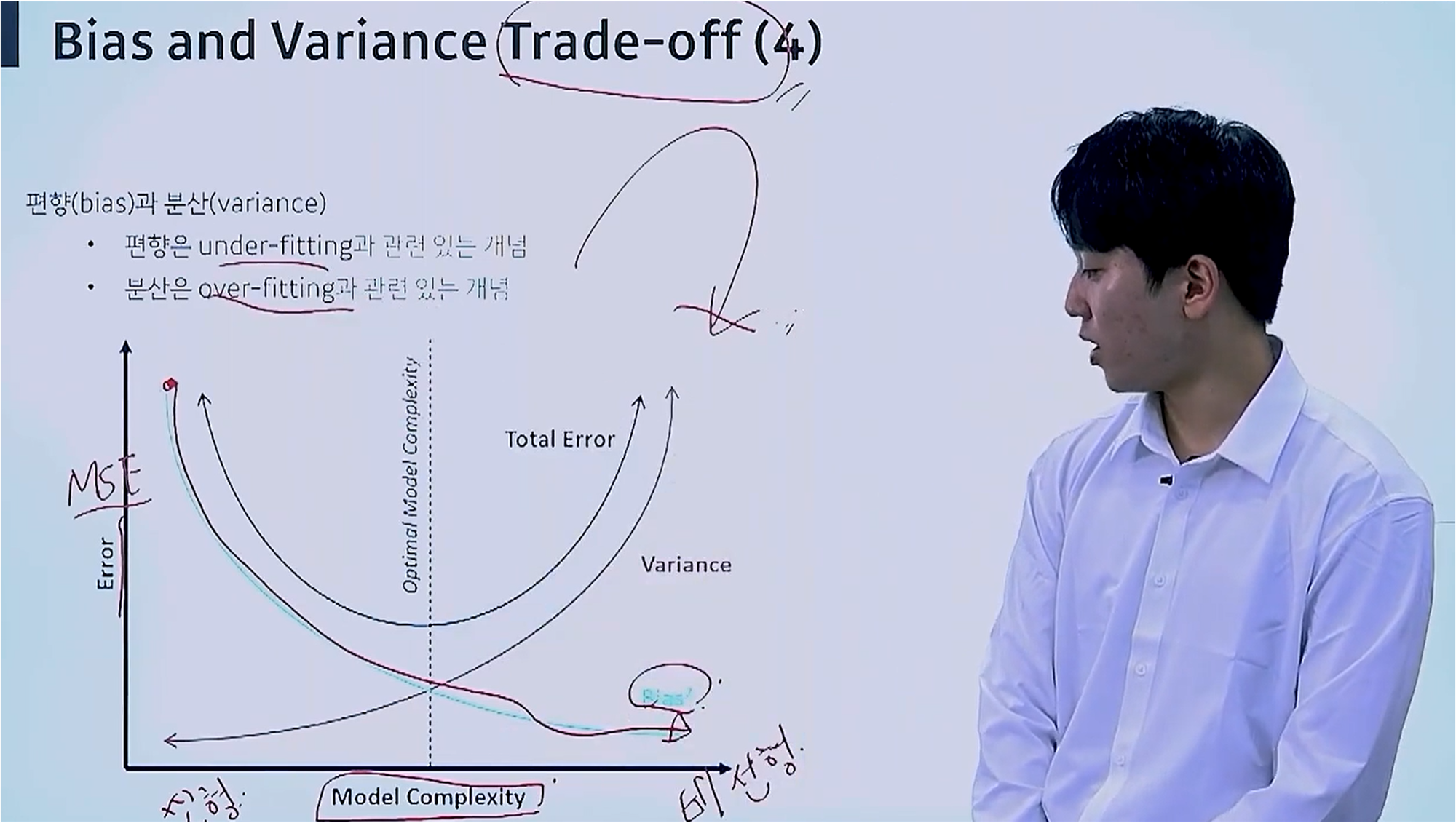
그래프에서 X축의 좌측은 선형 모델, 우측은 비선형 모델에 해당합니다.
모델의 복잡도가 낮을수록, 즉 선형 모델에 가까울수록 편향값은 커지지만 Variance 값은 작은 모습을 보입니다.
모델이 단순하기 때문에 에러가 발생하더라도 일정한 모습을 보이고, 이로 인해 Variance 값이 작습니다.
대신 선형 모델에서는 파라미터가 적기 때문에 편향값은 커집니다.
똑같은 데이터셋이 들어올 때 모델의 복잡도가 커지면, Under-fitting이 발생하고 이는 편향에 영향을 주며, 분산은 반대로 Over-fitting이 발생합니다.
'인공지능 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "1단원 실습" (0) | 2024.07.28 |
|---|---|
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Validation Data" (0) | 2024.07.27 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Gradient Descent" (3) | 2024.07.20 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "기초수학 ~ 최소제곱법" (3) | 2024.07.14 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "강좌 소개 ~ 기초 수학" (1) | 2024.07.14 |