하나둘셋넷

[통계 기초의 모든것 올인원] 메타코드 강의 후기 - 모분산, 두 집단 비교

메타코드M (metacodes.co.kr)

모분산 검정의 필요성, 예시

모분산 검정은 두 가지 집단이 모평균의 차이가 있냐 없냐를 판단할 때 중요하다.

왜냐하면, 그러한 검정은 두 집단의 모분산이 같다가 전제되어야 하기 때문이다.

등분산 조건을 의미한다.

이 문제에서 대립 가설은 분산이 0.1보다 작다는 것이 된다.

확률 표현은 오른쪽 영역을 기준으로 한다.

기각역은 10.117이 되는데 검정통계량 계산량은 9.5가 되므로 귀무가설을 기각할 수 있게 된다.

집단 비교

두 집단의 비교에는 분산이 고려되어야 한다는 것이 중요한 포인트이다.

분산이 고려되었을 때 객관적 비교가 가능하기 때문이다.

모분산은 아는데, 정규 모집단이면 Z 통계량을 사용한다.

모분산은 모르는데, 정규 모집단이긴 하다면,

모분산이 같은지 혹은 모분산이 다른지 확인하는 절차가 필요하다.

모분산 아는 경우의 모집단 비교

정규모집단 가정이 되어있는 상태이다.

기댓값 E의 경우 하나의 항에서 두 개의 항으로 분리가 가능하다.

이때, 각각의 기댓값은 뮤이다.

Variance는 분해를 할 때, 독립이라는 전제가 되어있다면 분해가 가능하다. 이때, 괄호 안이 + 부호이든 - 부호이든 더하기 형태로 분해된다.

모집단 비교 - 예시 #1

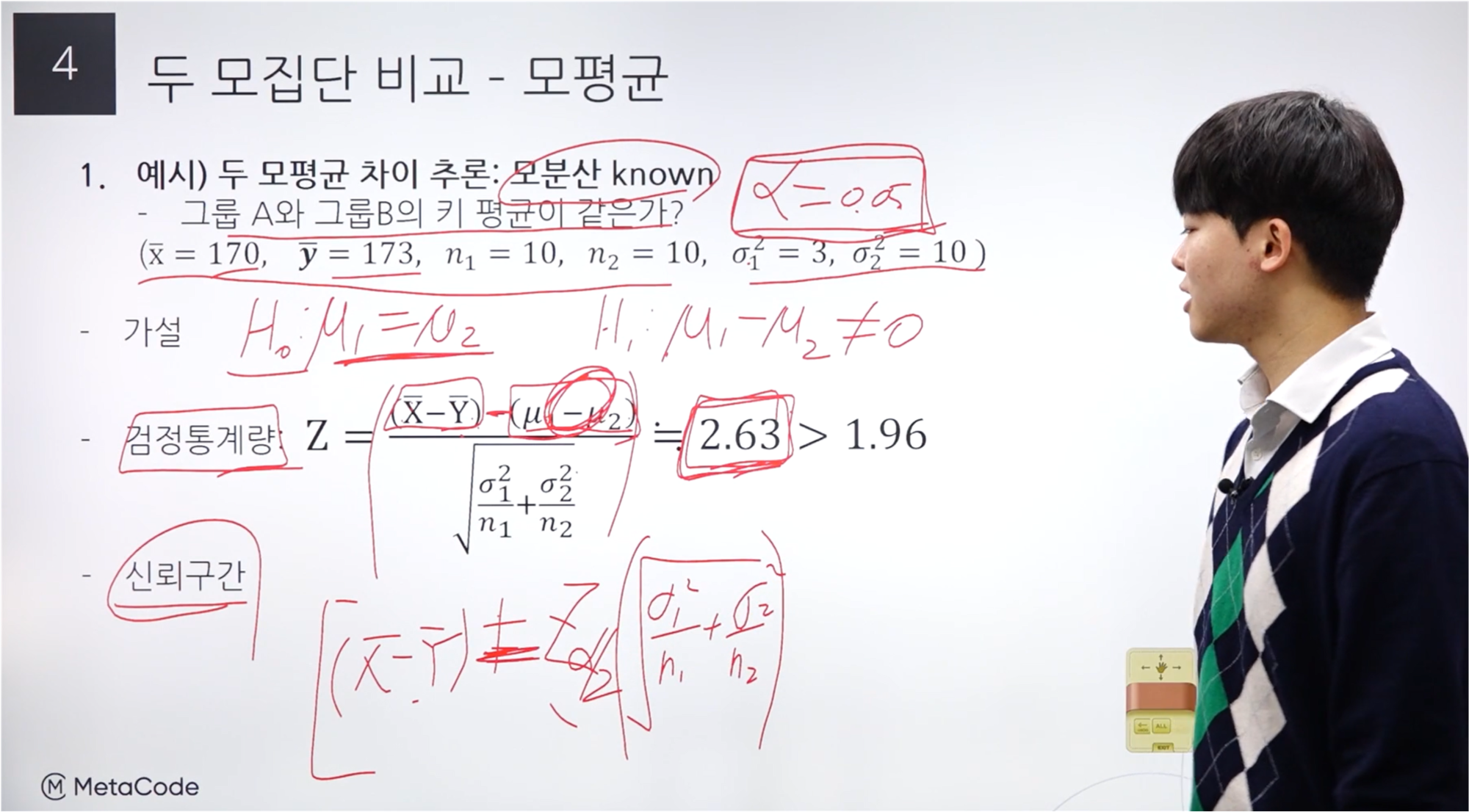
문제 조건에서 모분산을 알고 있다고 가정한다.

같은 지 물어보는 것이기 때문에 양측 검정에 해당한다.

대립 가설은 키 평균이 같지 않다는 것이 된다.

검정 통계량 식은 윗 슬라이드에 있던 내용이다.

검정은 귀무가설의 입장을 기준으로 한다. 즉, 일단 귀무 가설의 말이 맞다고 가정한다는 의미이다.

뮤 1과 뮤2는, 귀무가설이 “평균이 같다”이므로 0이 된다.

계산 결과가 2.63이므로 귀무가설을 기각할 수 있게 된다.

모집단 비교 - 예시 #2

t 통계량을 사용하는 경우의 문제이다.

귀무가설은 평균이 같다는 경우가 되고, 대립 가설은 같지 않다가 된다.

같지 않다가 조건이므로 양측 검정에 해당하며 ( 알파 / 2 ) 값을 확인한다.

이 문제에서는 계산 결과가 유의수준보다 크기 때문에 귀무가설을 기각할 수 있게 된다.

슬라이드에서 검정 통계량에 Z 가 아니라 T로 수정해야 한다.

모집단 비교 - 예시 #3

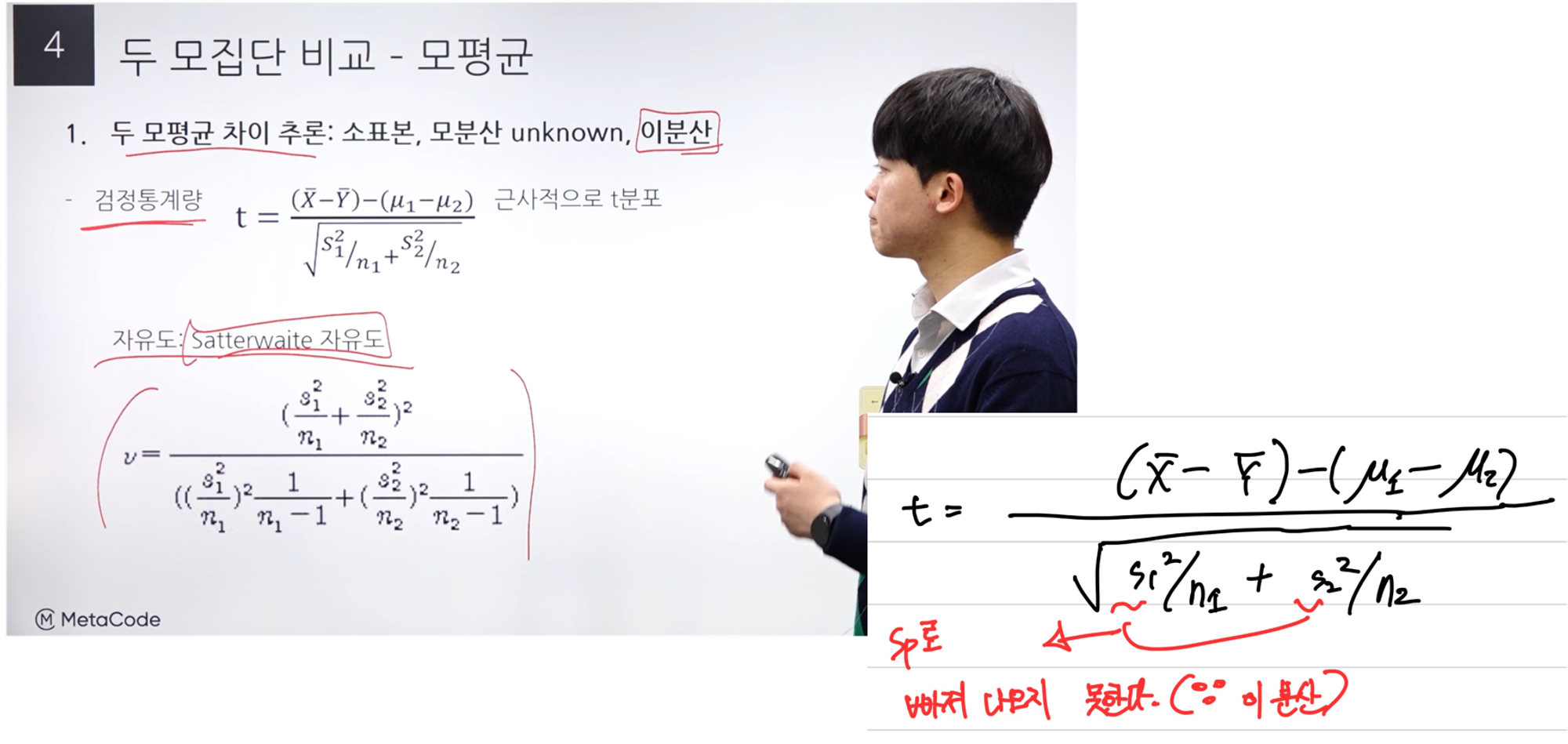
다른 조건은 같지만 분산이 다른 경우이다.

이분산인 경우에는 t 검정 통계량을 사용한다.

이분산이기 때문에 검정 통계량 식에서 s1, s2가 빠져나오지 못한다는 것이 앞의 문제와 차이이다.

밑의 자유도 식은 뒷 과정에서 다룰 것이다.

[통계 기초의 모든것 올인원] 메타코드 강의 후기 - 검정

https://mcode.co.kr/video/list2?viewMode=view&idx=94

가설검정 정리

일반적으로 제 1종 오류가 더 중요하다.

신약을 예시로 들면 좀 더 이해하기 편하다.

귀무가설이 "신약이 기존 약과 큰 약효의 차이가 없다"라고 했을 때,

제 1종 오류를 범한다면 신약이 약효가 있음에도 없다고 하는 것이 된다. 비즈니스적으로는 불리한 점이 생기지만 치명적인 문제는 생기지 않게 된다.

검정 - 요소

p-value는 데이터에서 계산하는 것이다.

미리 지정해둔 값 알파보다 계산된 p-value가 크다면 귀무가설을 기각한다.

예시) 알파가 0.05라면, p-value가 0.05 미만으로 나온 상황에서는 귀무가설을 기각한다.

기각역과 채택역에서는 검정통계량의 관측값이 어디에 속하는지 확인하고, 기각역에 속한다면 귀무가설을 기각한다.

검정의 종류

양측 검정에서는 양쪽에 있는 너비의 합이 알파가 되도록 한다.

즉, 각각의 영역의 너비는 ( 알파 / 2)이다.

단측 검정에서는 한 쪽에 있는 영역의 너비가 알파가 되도록 한다.

양측 검정에서는 같지 않다, 단측 검정에서는 크다 혹은 작다로 부등호를 정한다.

검정 - 모평균 검정, 표본의 크기가 큰 경우

표본의 크기가 크다면, 모분산을 알든 모르든 Z 검정 통계량을 사용할 수 있다.

다만, 모분산을 아냐 모르느냐에 따라 모평균(시그마)를 사용할지 표본평균(S)를 사용할지는 나뉘게 된다.

표본이 크기 때문에 x bar 자체는 정규분포를 따르게 된다.

계산된 Z 값을 아래의 표에 따라 적용하면 귀무가설을 채택할지 기각할지를 정할 수 있다.

검정 - 모비율 검정 예제

발병률이 3%인데, 100명( n=100 )을 대상으로 조사하니 2명으로 확률보다 더 낮게 나온 상황이다.

이 문제는 이항검정법으로 접근한다.

알파가 0.05로 나왔으니, 임계값 c를 찾는 것이 목표이다.

e 위에 지수가 3인 이유는 np로 계산하기 때문이다. n = 100이고, p = 0.03이므로 계산 결과는 3이 된다.

모비율 검정

"p0", "q0"는 귀무가설이 맞다는 가정에서의 값을 말한다.

분자에서는 P에 대한 기댓값이 "p0"라는 가정으로 빼는 과정을 수행하는 것이다.

분모에서도 마찬가지 논리로 Standard Error를 계산하는 것이다.

예시로는, "상대방 말이 맞다는 전제 하에서 논리를 전개해보고 오류가 생기는지 확인하는 것이다"를 들어주었다.