[메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Logistic Regression"
머신러닝 입문 부트캠프ㅣKAIST AI 박사과정
www.metacodes.co.kr
안녕하세요 메타코드 서포터즈 5기로 활동하고 있는 송주영입니다.
날씨가 습해서 아침에 출발할 때는 항상 손선풍기를 챙기게 되네요ㅠ
이번 글을 마지막으로 서포터즈 5기 활동을 마무리하게 되었습니다.
저는 서포터즈 6기로도 지원할 예정이니, 또 좋은 뵙고 싶습니다
강의 리뷰 시작하겠습니다!!
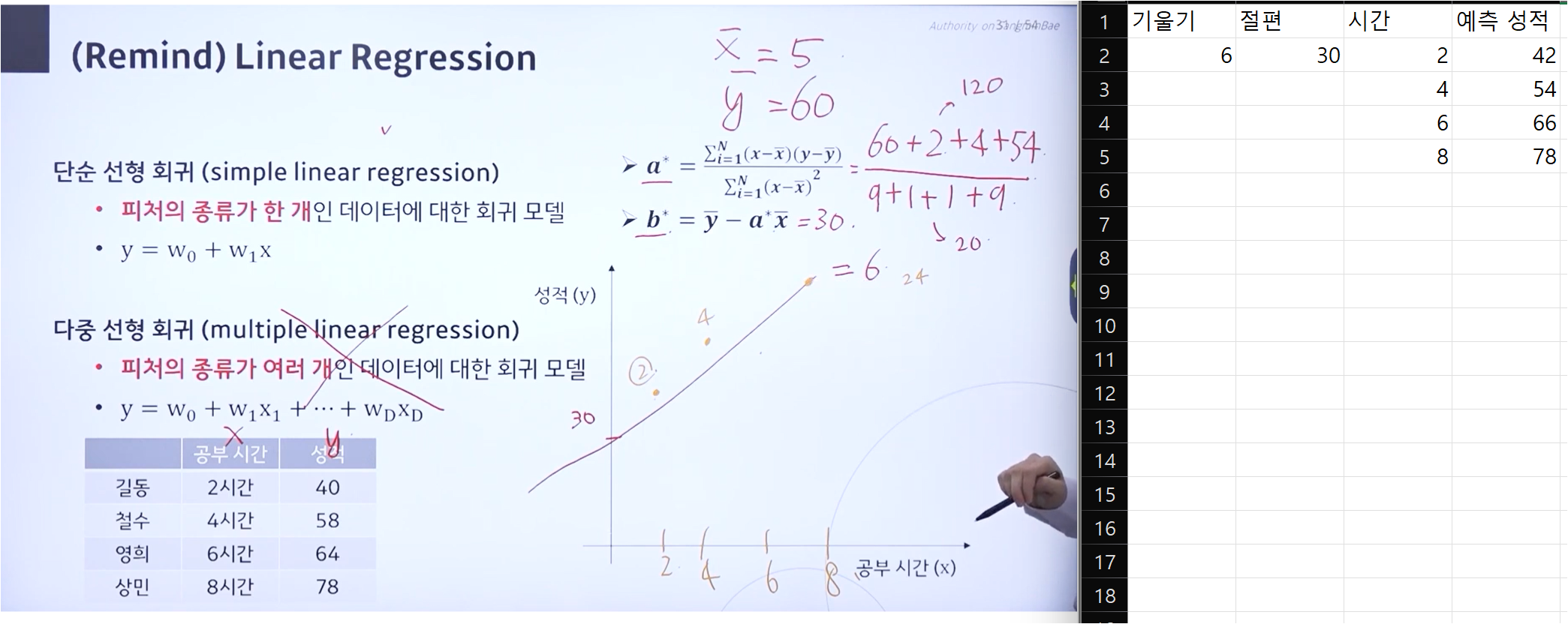
복습 Regression vsv Classification

회귀와 분류에 대한 복습입니다.
두 모델 모두 입력값으로는 연속값, 이산값을 취할 수 있습니다.
두 모델은 출력값에서 차이를 갖게 되는데, 회귀 모델은 연속값을 출력값으로 갖고 분류 모델은 이산값을 출력값으로 갖습니다.
분류 모델은 이진 분류인지, 다중 분류인지에 따라 시그모이드 함수를 포함할지, 소프트맥스 함수를 포함할지 정합니다.
Sigmoid Function

시그모이드 함수는 입력이 없을 때는 출력값이 0.5입니다.
입력이 들어오게 된다면, 그 값은 0 혹은 1에 가까운 값이 됩니다.
완벽하게 0 혹은 1로 분류되는 것이 아니기 때문에 완만한 곡선 형태를 보입니다.
이진 분류에서는 시그모이드 함수 개념을 사용합니다.
오즈, 로짓 변환(logit)

오즈는 성공 확률이 실패 확률에 비해 몇 배나 더 높은지 나타내는 개념입니다.
수식으로는 p(y=1|x)1−p(y=1|x)=p(y=1|x)p(y=0|x)와 같이 표현할 수 있습니다.
성공 확률 + 실패 확률 = 1이므로, 실패 확률 = 1 - 성공확률로 표현 가능합니다.
로짓 변환은 오즈에 로그를 취한 것으로, 오즈 수식 앞에 log가 붙은 것을 확인할 수 있습니다.
로지스틱 함수

로지스틱 함수는 로짓 변환의 역함수로 해석 가능합니다.
역함수의 개념은 y = x를 기준으로 대칭인 함수입니다.
계산 과정에서, (logp1−p)−1=ep1−p에 따라 식을 전개했습니다.
좌항에 p에 대한 식을 모아서 정리하고 연산을 수행하여 p에 대한 식을 구했습니다.
로지스틱 회귀

로지스틱 회귀는 로지스틱 함수를 활용하여 값을 예측합니다.
로지스틱 함수를 사용하므로 연속적인 값(=실수값)을 반환합니다.
입력값이 양수인지, 음수인지에 따라 값이 1과 0으로 분류됩니다.
이러한 값의 분류는 e−wTX 항을 생각하면 쉽게 이해할 수 있습니다.
Bayes' Theorem

베이즈 정리에는 사후 확률, 우도 확률, 사전 확률 개념이 있습니다.
사후 확률이란, 식을 보면 X에 대하여 w가 일어날 확률로 해석하면 데이터가 주어졌을 때 가설에 대한 확률 분포를 말합니다.
우도 확률은 데이터가 어느 쪽으로 쏠려있는 지를 보는 개념입니다,
사전 확률은 이미 알고 있는 확률로 일반적으로 사용하는 확률 개념입니다.
'인공지능 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "1단원 실습" (0) | 2024.07.28 |
|---|---|
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Validation Data" (0) | 2024.07.27 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Bias and variance Trade-off" (0) | 2024.07.21 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "Gradient Descent" (3) | 2024.07.20 |
| [메타코드 강의 후기] 메타코드 머신러닝 입문 부트캠프 - "기초수학 ~ 최소제곱법" (3) | 2024.07.14 |