[메타코드 강의 후기] 통계 기초의 모든것 올인원_회귀분석_Part2_240630
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
안녕하세요
메타코드 서포터즈 5기 송주영입니다.
한 주를 마무리하면 지금까지 듣던 "통계 기초의 모든 것 올인원" 강의를 완강하게 되어 뿌듯함을 느꼈어요
ADsP 자격증을 따면서 기초적인 통계를 배우기는 했지만 이렇게 하나의 강의를 온전히 들으니 자격증에서는 배우지 못한 내용들을 배울 수 있어서 좋았어요
만약 비전공이시거나, 비전공 출신으로 자격증은 취득했으나 아직 통계 개념이 어렵다면 메타코드 통계 강의를 들어보면서 큰 틀을 잡아보시는 것도 좋을 거라 생각해요
"통계 기초의 모든것 올인원_회귀분석_Part2" 강의 후기 작성하겠습니다.
잔차제곱합, MSE

ˆy 추정회귀식에 해당한다.
이를 풀어서 작성하면 “베타 0 hat”, “베타 1 hat”, “x i”를 통해 작성할 수 있다.
MSE는 SSE를 자유도로 나눈 값을 말한다.
“시그마 제곱 hat”으로 표시하며, 오차분산의 불편(unbiased) 추정량이다.
β1의 추정 및 검정(1)

“a i”라는 새로운 term을 하나 만들었으며, 이 식은 아래 추정 및 검정 과정에서 사용된다.
“베타 1”에 대한 추정과 검정을 하는 것이 목표이다.
이러한 추정과 검정을 할 때는 항상 기댓값과 Variance를 구하는 과정을 수행했으며, 이 경우에도 마찬가지이다.
“베타 1 hat”에 대한 식은 값들을 차례로 대입하고 나누어주는 과정을 수행하여 구한다.
“베타 1 hat” 식의 마지막 부분에서 “베타 0”에는 “a i”에 해당하는 값의 summation이고, “베타 1”에는 ‘a i”값의 summation에 “x i”가 곱해져 있다.
“a i”의 summation의 값은 0이고, “베타 1”에 곱해져 있는 부분은 1이 되므로 최종적으로 “베타 1 hat”에 대한 값은 “베타 1”이 된다.
“a i”의 summation 식을 보면 분자값이 0이 되게 되므로 전체 값이 0이 된다.
β1의 추정 및 검정(2)

“a i hat”의 제곱식을 대입한 뒤 정리하면 분자가 “시그마 제곱” 형태가 된다.
“시그마 제곱”의 불편추정량은 MSE에 해당한다.
“베타 1 hat”에 대한 Variance 값은 자유도가 (n-2)인 t 분포를 따른다.
신뢰구간을 설정한다면 양측 검정이므로 “베타 1 hat”에 똑같은 식을 +, -를 해준다.
이때 양측 검정이므로 알파 값의 1/2에 해당하는 사용한다.
β0 의 추정 및 검정
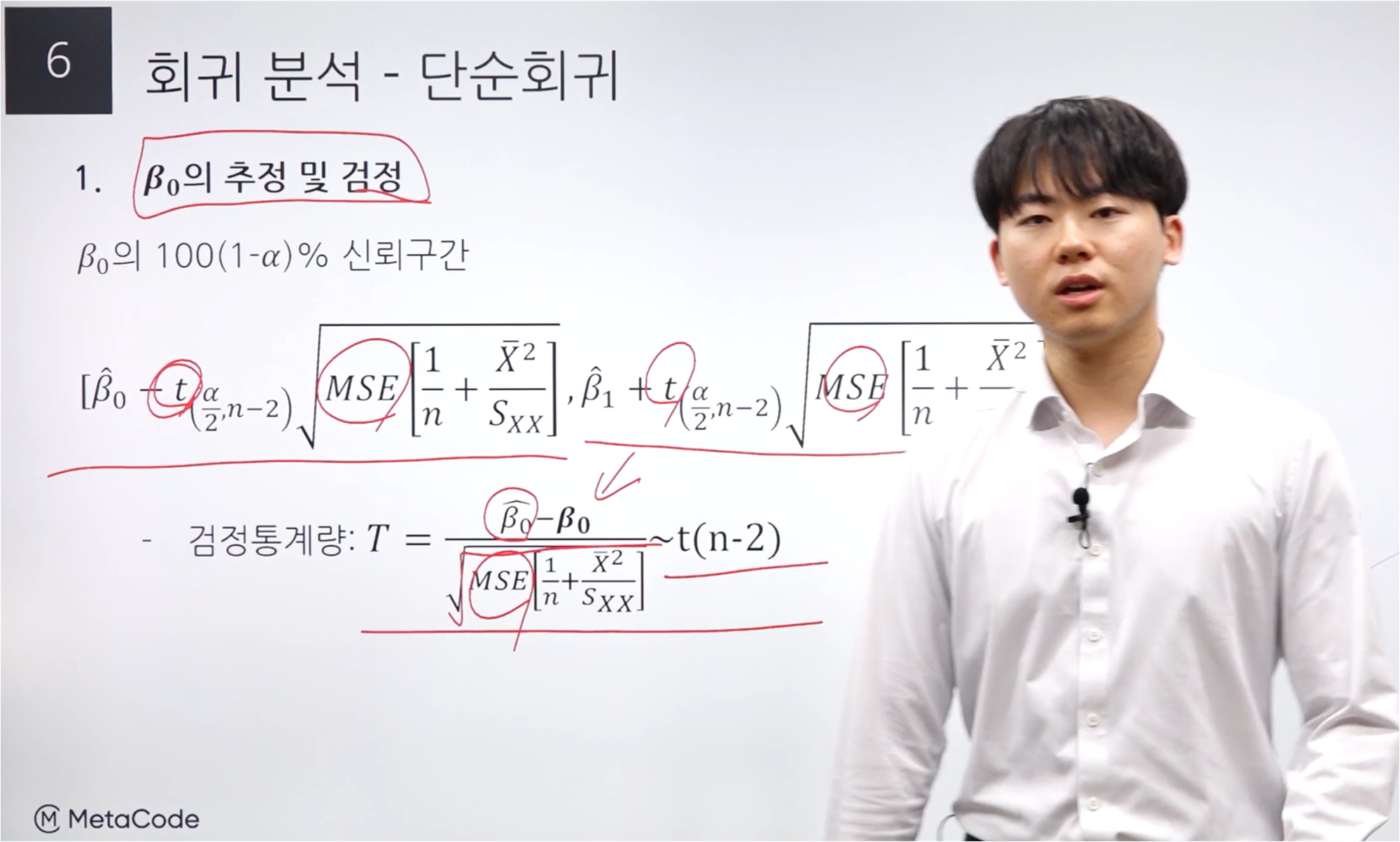
“시그마 제곱”은 “MSE”에 해당하므로, “시그마 제곱” 값을 모른다면 “MSE”를 구하여 사용한다.
검정통계량에서 분모 부분은 Standard Error이며, “시그마 제곱”를 모르기 때문에 “MSE”를 넣었다.
분자는 “베타 0 hat”에서 “베타 0 hat”의 기댓값인 “베타 0”를 빼준다.
이렇게 구한 검정통계량 값은 자유도가 (n-2)인 T 분포를 따른다.
변동분해, 분산분석

총 변동 yi−¯y 식은 개별관측값과 이에 대한 평균의 차이다.
식에서 각 항을 제곱하면, 설명이 안되는 변동은 잔차제곱합 SSE가 되고 설명이 되는 변동은 회귀제곱합 SSR이 된다.
자유도는 총 변동, 잔차변동, 회귀변동이 각각 (n-1), (n-2), n이다.
각각의 자유도로 나누어주면 MSE와 MSR 값을 구할 수 있다.
회귀모형 검정_F 검정
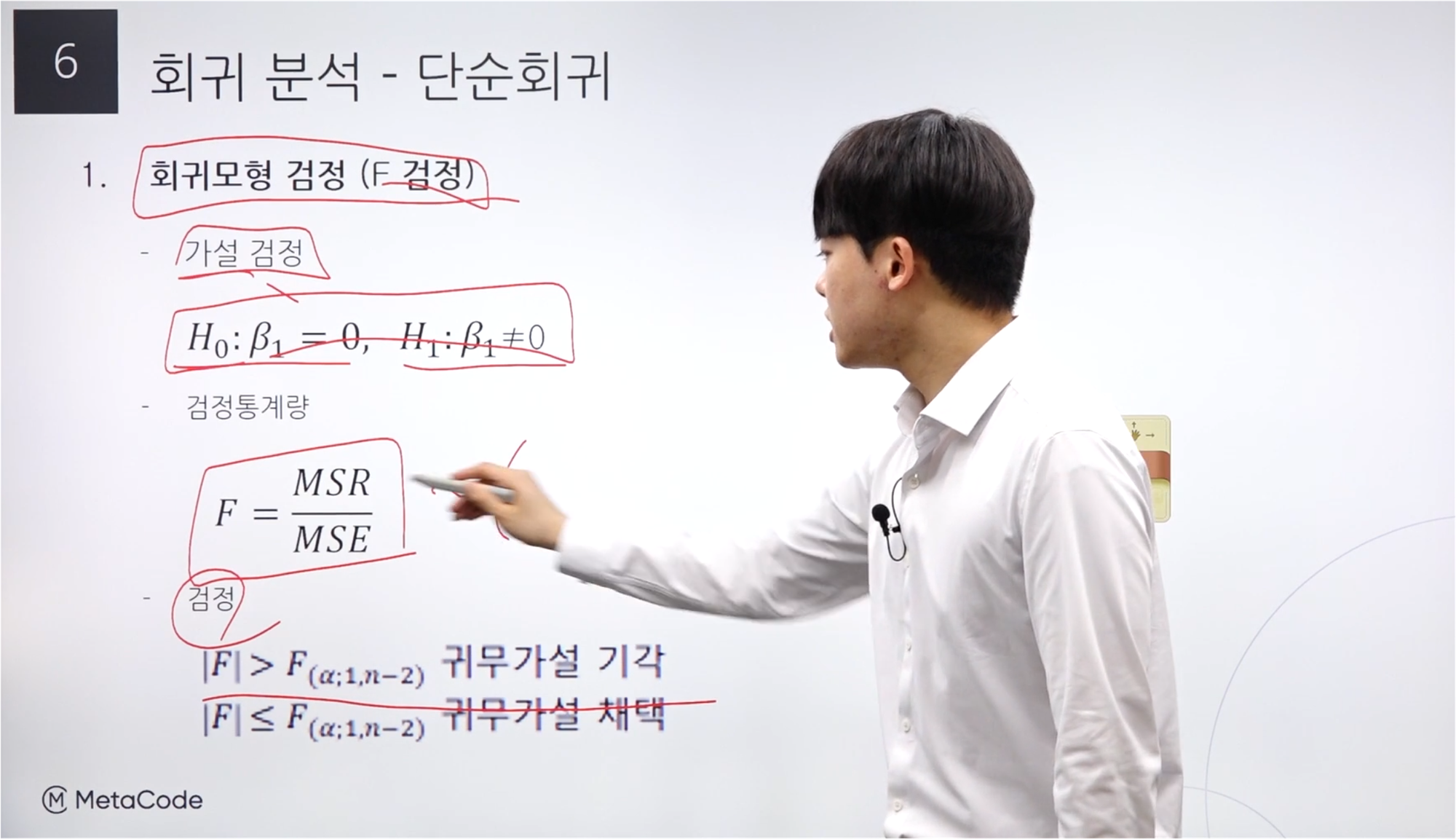
단순 선형회귀에서는 “베타 1 = 0”이 귀무가설이다.
만약 다중 선형회귀가 된다면 베타 1, 베타 2, 베타 3, ..으로 늘어난다.
F 통계량 식에서 MSR은 자유도가 1, MSE는 자유도가 (n-2)이다.
단측검정이므로 유의수준 알파를 그대로 사용한다.
강의를 완강하며, 어려운 점들도 있었지만 선생님께서 쉬운 예시를 들어주셔서 따라갈 수 있었던 것 같아요.
진도의 뒷 부분에 도달하니 앞 부분에서 내가 어떤 개념을 덜 이해하고 넘어갔는지 체감할 수 있었고, 이에 대해 다시 복습할 필요성을 느꼈습니다.
다음 수업으로는 Python을 활용하여 통계 이론을 실습하는 수업을 할지 아니면 다른 수업을 들을지 고민이 드네요
현재 생각으로는 그래도 실습을 하며 배운 개념을 계속하여 적용하다 보면 통계 개념에 익숙해지고 이해가 되지 않을까 생각을 하고 있습니다.
이상으로 "통계기초의 모든 것 올인원" 강의 후기는 마무리하도록 하겠습니다.
감사합니다!!
'통계 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 통계 기초의 모든것 올인원_회귀분석_Part1_240629 (0) | 2024.06.30 |
|---|---|
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 이원배치 분산분석_240623 (0) | 2024.06.23 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 일원분산분석_240623 (0) | 2024.06.23 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 대응비교, 모비율, 모분산 비교_240616 (0) | 2024.06.16 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 모분산, 두 집단 비교_240616 (1) | 2024.06.16 |

















