[메타코드 강의 후기] 통계 기초의 모든것 올인원 - 일원분산분석_240623
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
안녕하세요 메타코드 서포터즈로 활동하고 있는 송주영입니다.
저는 작년 하반기부터 데이터 분석가의 꿈을 꾸고 이 분야를 공부하기 시작했어요.
메타코드는 데이터 분석, 인공지능 등 다양한 분야의 강의를 제공하고 있는 강의 사이트입니다. 이 분야의 입문자들에게는 어떤 강의가 좋을지 직관적으로 안내해주는 것이 메타코드 사이트의 장점이라고 생각합니다. 꾸준히 이벤트도 진행하고 있으니 가벼운 마음으로 방문해보셔도 좋을거 같아요
요새 꾸준히 공부하기가 어려워서ㅠ 서포터즈 활동을 하면 보다 몰입감을 가지고 강의를 들을 수 있을거 같아서 시작했고, 메타코드가 성장하는 모습을 보니 간접적으로나마 기여했다는 생각이 들어서 뿌듯함 또한 느끼고 있습니다.
"통계 기초의 모든 것 올인원" 강의 중 일원배치 분산분석에 대한 강의 후기 작성해봤습니다.
분산분석, 기본가정

반응변수는 종속변수와 같은 개념이다.
인자의 경우 독립변수의 개념이며, 반응변수에 어떠한 영향을 주는지 알아보는 것이 목표이다.
MBTI를 예시로 들면, MBTI 하나하나의 특성이 “처리(treatment)” 개념의 수준의 개념이다. 즉 16가지의 수준이 존재
분석에 앞서서 정규분포, 등분산, 오차가 독립이다는 기본 가정을 확인해야 한다.
분산분석의 식과 종류

그룹 간 변동이 우리가 검정하고 싶은 내용이다.
즉 MBTI가 그룹별로 어떻게 나눠지는지 등의 내용을 말한다.
그룹내 변동은 말 그대로 같은 집단 안에서 어느 정도의 차이가 있는지를 말한다.
인자가 몇 개인지에 따라 “일원배치분산분석”인지 “이원배치분산분석”인지로 나뉜다.
“이원배치분산분석”의 경우 인자가 두 개이므로 이들의 교호 작용 또한 생각해야 한다.
일원배치 분산분석

일원배치 분산분석에서 k개의 모집단의 개념을 보면, k는 요인이 취할 수 있는 값의 개수를 말한다.
Unique한 값의 개수를 말한다.
앞서 배웠던 기본 가정대로 각 집단은 독립이고 정규분포를 따라야 한다.
분산은 같아야 하지만, 평균은 다를 수 있음을 유의해야 한다.(*MBTI를 예시로 생각하면 이해가 쉽다)
반복수가 같은 경우의 일원배치 분산분석 표

반복수 : 특정 처치를 가할 때 그 안에 그룹이 몇 개가 있는가?
예시로는 “MBTI 별로 그 집단 안에 몇 명이 있는지”를 들 수 있다.
처리별로 본다면 각 처리별로는 크기가 n으로 동일하다.
y11에서 앞 부분이 k에 해당하고 뒷 부분의 숫자가 샘플의 숫자를 의미한다.
입실론은 개별 관측값이 가질 수 있는 오차를 말한다.
일원배치의 관찰값 모형
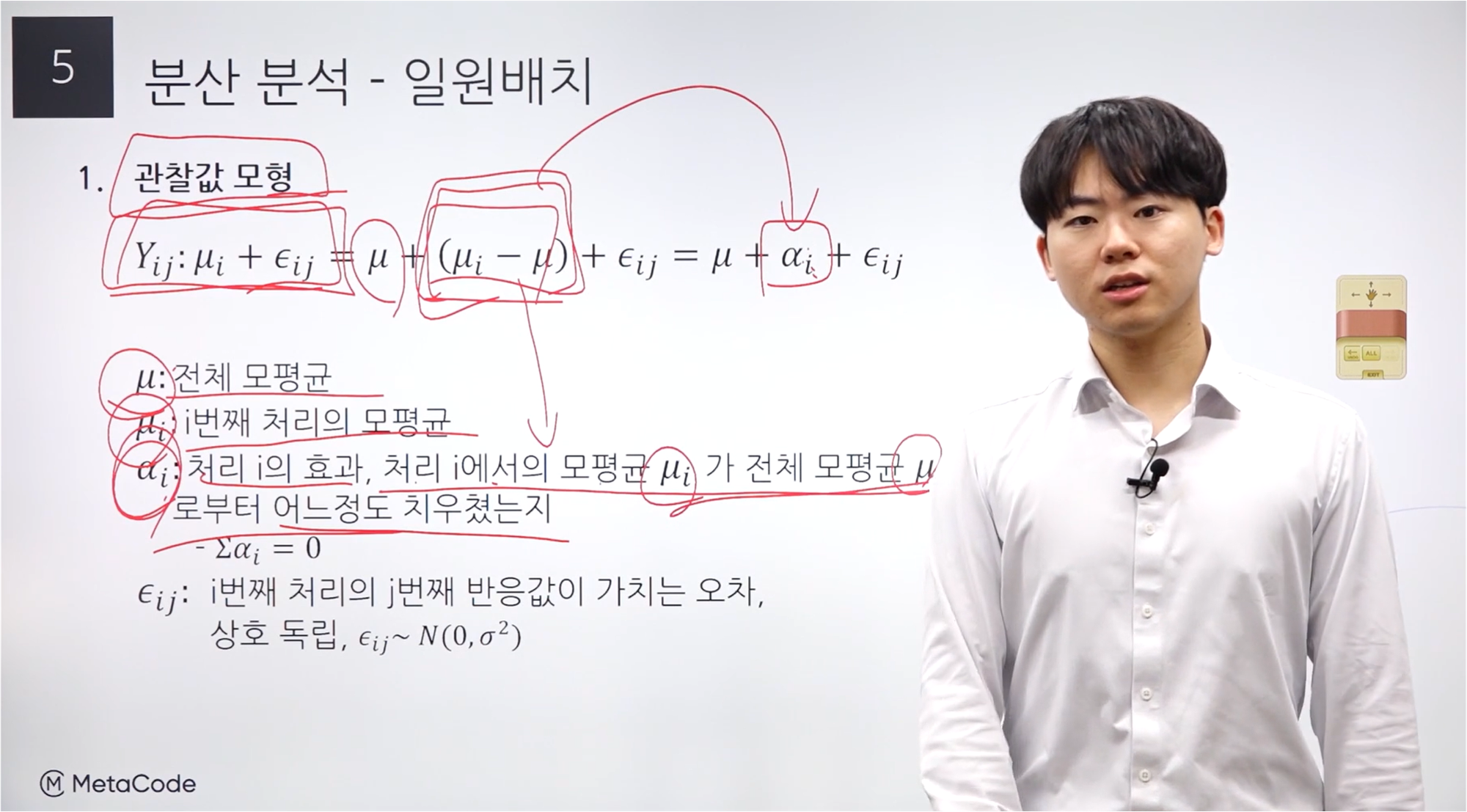
알파 i 가 우리가 관심을 가져야 하는 대상이다.
알파 i는 MBTI라고 한다면, 그 안의 특성이 어느 정도의 영향을 주는 지를 말한다.
모평균과 전체 모평균과의 차이가 얼마나 나는지를 확인하면 영향력을 파악할 수 있다.
수식을 관찰하면, 위 식에서 ( 뮤 i - 뮤 ) = ( 알파 i )가 된다.
일원배치 분산분석에서 오차항 가정의 중요성

분산분석을 진행한 이후에는 오차항에 대해 집중적으로 검증을 한다.(=잔차 진단)
오차항이 아래의 4가지 조건을 모두 만족하는 지를 확인하는 과정을 말한다.
오차가 있어야 분석이 의미있는 것이기 때문에, 오차항 검증이 중요성을 갖는다.
귀무가설 식에서 ( 뮤 i )와 ( 알파 i )가 같은 것은 관찰값 모형식에서 보면 ( 뮤 )는 하나의 상수값으로 볼 수 있기 때문이다.
제곱합 분해

식의 각 부분을 구분하자면 앞 부분은 처리 효과에 대한 값이고 뒷 부분은 잔차에 대한 값이다.
식에서 SST는 Sum of Squares Total로 잔차들의 총합을 말하고,
처리간 분산 SSt는 Sum of Squares Treatment로 처리 효과의 합,
처리 내 분산 SSE는 Sum of Squares Error로 잔차에 대한 값이다.
평균 제곱
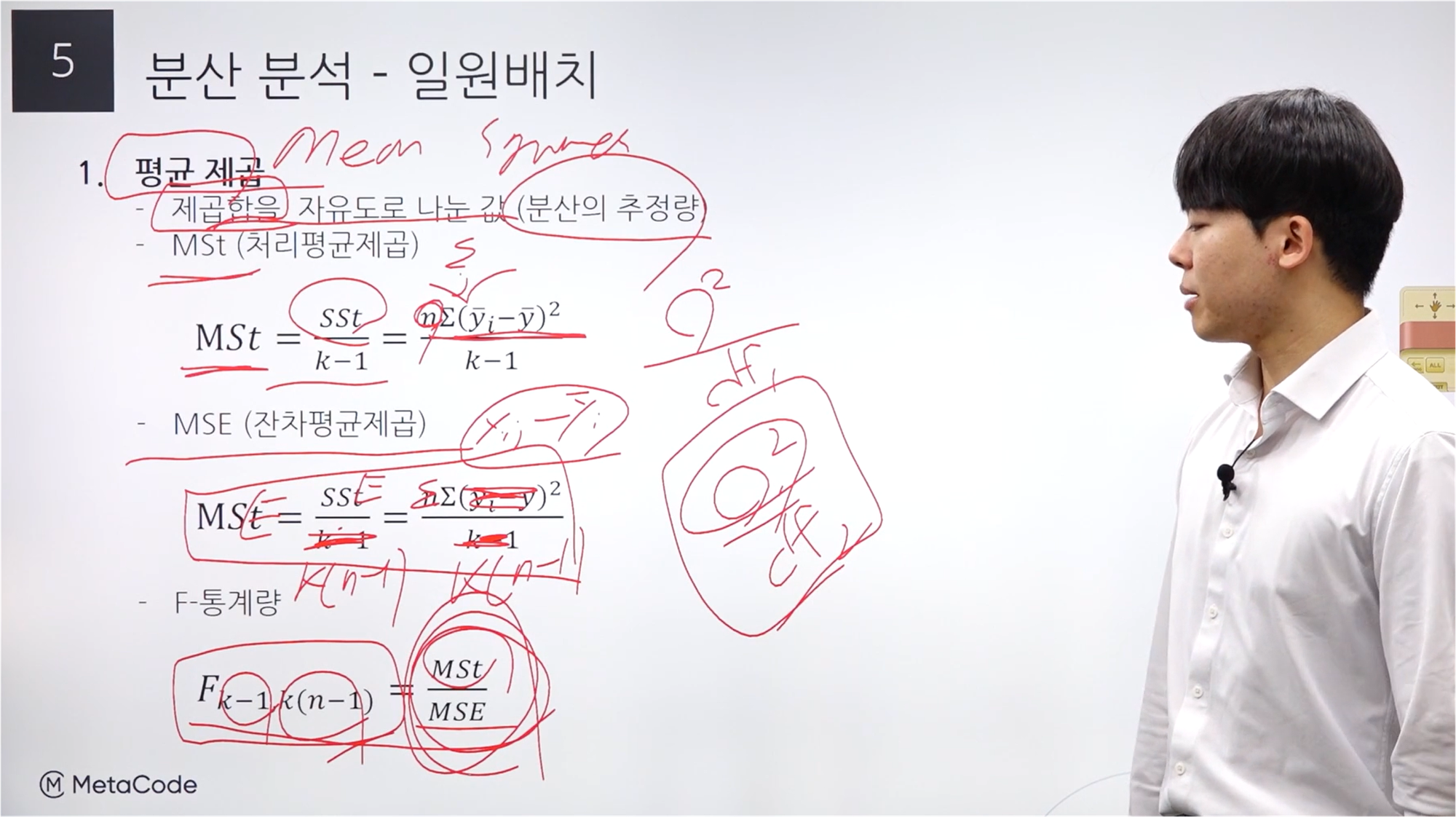
평균제곱은 Mean Squares total로 제곱합에서의 값을 자유도로 나눈 값을 의미한다.
평균제곱은 뷴산의 추정량(분산 estimator)에 해당한다.
목표는 집단 내 효과가 집단 간 효과보다 큰 것인가를 알아내는 것이다.
처리에 의한 효과가 더 커야 분산분석이 의미를 갖는다.
강의후기
이번 강의에서는 수식과 각 수식에 대한 Notation이 많아서 집중을 하지 않으면 흐름을 놓치지 쉬웠어요
공식에 대한 증명을 해주시고, 이해하기 쉽게 MBI를 예시로 들어주신 것이 큰 도움이 되었어요!!
비전공자에게 어려운 부분이 있기도 했지만, 설명이 자세하여 그래도 들을만 했던 거 같아요
서포터즈로서 글을 작성하다보니 수업 때 배운 내용을 정리할 수 있어서 좋았어요
'통계 - 메타코드' 카테고리의 다른 글
| [메타코드 강의 후기] 통계 기초의 모든것 올인원_회귀분석_Part1_240629 (0) | 2024.06.30 |
|---|---|
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 이원배치 분산분석_240623 (0) | 2024.06.23 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 대응비교, 모비율, 모분산 비교_240616 (0) | 2024.06.16 |
| [메타코드 강의 후기] 통계 기초의 모든것 올인원 - 모분산, 두 집단 비교_240616 (1) | 2024.06.16 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 검정 (0) | 2024.05.30 |











