[통계 기초의 모든것 올인원] 메타코드 강의 후기 - t분포/F분포, 점추정/구간추정
https://mcode.co.kr/video/list2?viewMode=view&idx=94
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
표본분포 - t 분포

모집단의 표준편차를 모르면, 모표준편차 대신 표본표준편차를 사용한다?
자유도가 높은 것이 좋은 것이다?
=> 그렇지 않다, 임의로 결정될 수 있는 것이 늘어남에 따라 컨트롤하기 어려워진다.
X가 동일한 분포에서 나온 확률표본인데, 시그마를 모른다면 표본분산을 대신 사용할 수 있다.
이때, 표준정규분포가 아니라 t 분포를 따르게 된다.
표본분포 - t 분포 특징 정리

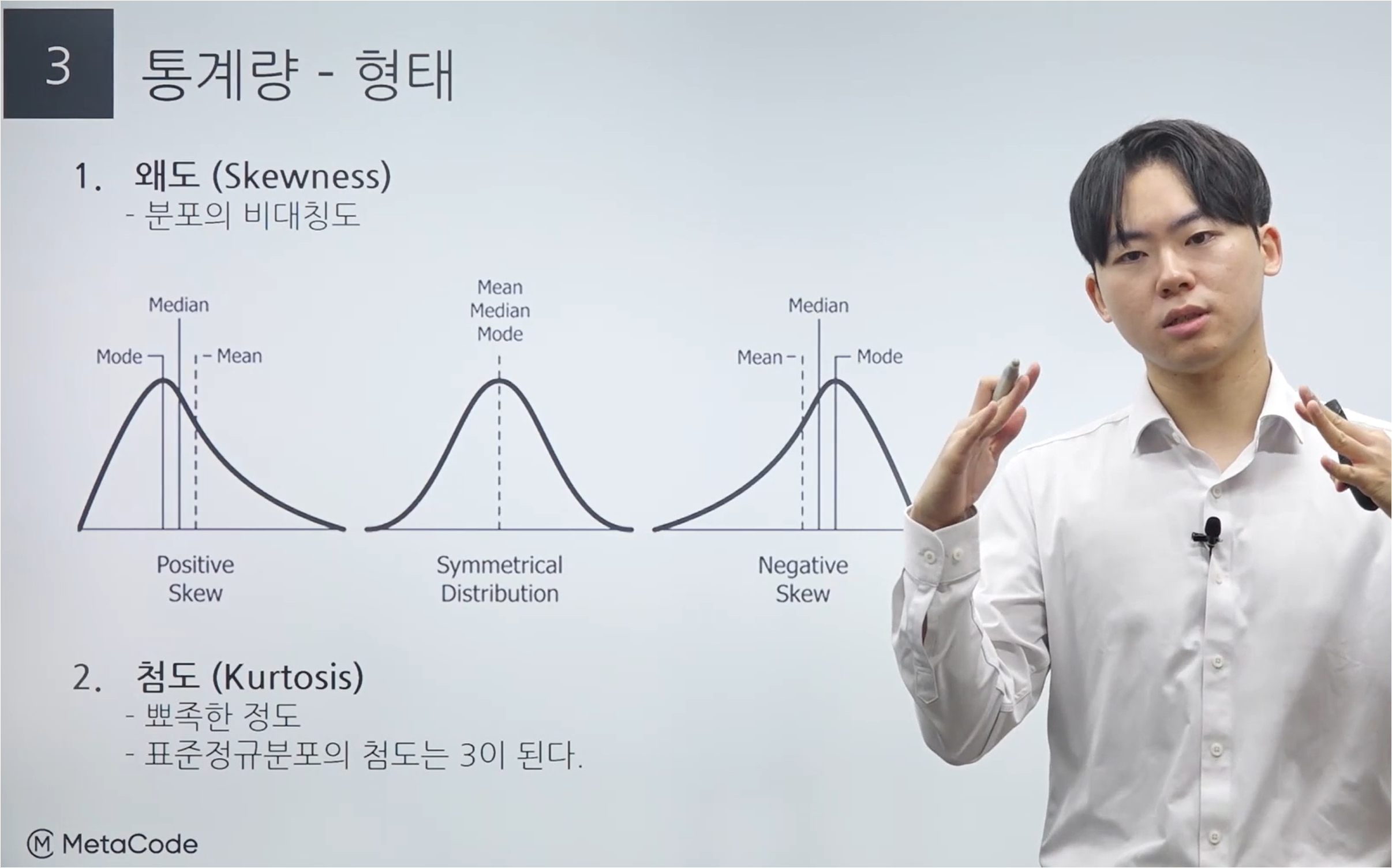
t 분포는 그림에서 볼 수 있듯이 정규분포보다 평평하게 나타나게 된다.
표본크기가 크다면, 분포가 중심부근에서 점점 뾰족해지는데 이때 표준크기가 30 이상이 된다면 정규분포에 근사하게 된다.
즉, 표본 30을 기준으로 이상이면 표준정규분포, 미만일 때는 t 분포가 된다.
t 분포는 모표준편차를 모르는 경우에 사용한다는 것이 가장 중요한 내용이다.
표본분포 - F 분포

V1을 본인의 모수로 나누어 주고, V2 또한 본인의 모수로 나누어 준다.
F 식에서 분자가 앞에 와야 한다는 것을 기억하자.
분산을 비교한다는 것은 회귀분석, 분산분석에서 중요하게 다루어지는 개념이다.
통계 분석에서 분산 분석은 가장 중요한 내용 중 하나이다.
표본분포 - 정리

정규분포는 모분산을 알고 있을 때, 모평균 혹은 두 모평균 차이에 대한 추정/검정을 할 때 사용한다.
이때, 모분산을 모르더라도 표본크기가 크다면 이를 동일하게 수행할 수 있다.
t 분포는 모분산을 모를 때 사용한다.
카이제곱분포는 모분산에 대한 추정/검정을 하고, F 분포는 두 모분산 차이에 대한 추정/검정에 사용한다.
점추정/구간추정

점 추정의 경우, 모수를 특정 값으로 추측한다.
신뢰도를 나타낼 수 없고, 오차에 대한 정보가 없다는 특징이 있다.
구간 추정은 점 추정과 달리, 모수를 특정 값이 아닌 구간으로 추정한다.
신뢰도를 나타낼 수 있다는 점이 점 추정과 다르다.
추정 - 점 추정

추정량(estimator)와 추정값(estimate)는 말은 비슷하지만 다른 개념이다.
이 강의에서는 추정량(Estimator)를 더 많이 사용할 것이다.
추정에서 사용되는 통계량을 통틀어서 통계량이라고 부른다.
추정값은 실제값을 의미한다. 즉 실제 계산된 결과를 말한다.
'통계 - 메타코드' 카테고리의 다른 글
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 구간추정/표본크기결정, 검정 (0) | 2024.05.29 |
|---|---|
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 점추정/구간추정 (1) | 2024.05.26 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 통계적 추정 (1) | 2024.05.19 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 연속확률분포, 통계적 추정 (0) | 2024.05.19 |
| [통계 기초의 모든것 올인원] 메타코드 강의 후기 - 연속확률분포 (0) | 2024.05.12 |